6 Multiple Regression

In Chapter 5, we studied simple linear regression as a model that represents the relationship between two variables: an outcome variable or response \(y\) and an explanatory variable or regressor \(x\). Furthermore, to keep things simple, we only considered models with one explanatory \(x\) variable that was either numerical in Section 5.1 or categorical in Section 5.2.

In this chapter, we introduce multiple linear regression, the direct extension to simple linear regression when more than one explanatory variable is taken into account to explain changes in the outcome variable. As we show in the next few sections, much of the material developed for simple linear regression translates directly into multiple linear regression, but the interpretation of the associated effect of any one explanatory variable must be made taking into account the other explanatory variables included in the model.

Needed packages

If needed, read Section 1.3 for information on how to install and load R packages.

library(tidyverse)
library(moderndive)
library(ISLR2)

6.1 One numerical and one categorical explanatory variable

We continue using the UN member states dataset introduced in Section 5.1. Recall that we studied the relationship between the outcome variable fertility rate, \(y\), and the regressor life expectancy, \(x\).

In this section, we introduce one additional regressor to this model: the categorical variable income group with four categories: Low income, Lower middle income, Upper middle income, and High income. We now want to study how fertility rate changes due to changes in life expectancy and different income levels. To do this, we use multiple regression. Observe that we now have:

1. A numerical outcome variable \(y\), the fertility rate in a given country or state, and
2. Two explanatory variables:
3. A numerical explanatory variable \(x_1\), the life expectancy.
4. A categorical explanatory variable \(x_2\), the income group.

6.1.1 Exploratory data analysis

The UN member states data frame is included in the moderndive package. To keep things simple, we select() only the subset of the variables needed here, and save this data in a new data frame called UN_data_ch6. Note that the variables used are different than the ones chosen in Chapter 5. We also set the income variable to be a factor so that its levels show up in the expected order.

UN_data_ch6 <- un_member_states_2024 |>
  select(country, 
         life_expectancy_2022, 
         fertility_rate_2022, 
         income_group_2024)|>
  na.omit()|>
  rename(life_exp = life_expectancy_2022, 
         fert_rate = fertility_rate_2022, 
         income = income_group_2024)|>
  mutate(income = factor(income, 
                         levels = c("Low income", "Lower middle income", 
                                    "Upper middle income", "High income")))

Recall the three common steps in an exploratory data analysis we saw in Subsection 5.1.1:

1. Inspecting a sample of raw values.
2. Computing summary statistics.
3. Creating data visualizations.

We first look at the raw data values by either looking at UN_data_ch6 using RStudio’s spreadsheet viewer or by using the glimpse() function from the dplyr package:

glimpse(UN_data_ch6)

Rows: 182
Columns: 4
$ country   <chr> "Afghanistan", "Albania", "Algeria", "Angola", "Antigua and Barbuda", "Argentina", "Armenia", "Austr…
$ life_exp  <dbl> 53.6, 79.5, 78.0, 62.1, 77.8, 78.3, 76.1, 83.1, 82.3, 74.2, 76.1, 79.9, 74.7, 78.5, 74.3, 81.9, 75.8…
$ fert_rate <dbl> 4.3, 1.4, 2.7, 5.0, 1.6, 1.9, 1.6, 1.6, 1.5, 1.6, 1.4, 1.8, 1.9, 1.6, 1.5, 1.6, 2.0, 4.7, 1.4, 2.5, …
$ income    <fct> Low income, Upper middle income, Lower middle income, Lower middle income, High income, Upper middle…

The variable country contains all the UN member states. R reads this variable as character, <chr>, and beyond the country identification it will not be needed for the analysis. The variables life expectancy, life_exp, and fertility rate, fert_rate, are numerical, and the variable income, income, is categorical. In R, categorical variables are called factors and the categories are factor levels.

We also display a random sample of 10 rows of the 182 rows corresponding to different countries in Table 6.1. Remember due to the random nature of the sampling, you will likely end up with a different subset of 10 rows.

UN_data_ch6 |> sample_n(size = 10)

TABLE 6.1: A random sample of 10 out of 182 UN member states

country	life_exp	fert_rate	income
Trinidad and Tobago	75.9	1.6	High income
Micronesia, Federated States of	74.4	2.6	Lower middle income
North Macedonia	76.8	1.4	Upper middle income
Portugal	81.5	1.4	High income
Madagascar	68.2	3.7	Low income
Cambodia	70.7	2.3	Lower middle income
Dominica	78.2	1.6	Upper middle income
Peru	68.9	2.1	Upper middle income
Cyprus	79.7	1.3	High income
Guinea-Bissau	63.7	3.8	Low income

Life expectancy, life_exp, is an estimate of how many years, on average, a person in a given country is expected to live. Fertility rate, fert_rate, is the average number of live births per woman of childbearing age in a country. As we did in our exploratory data analyses in Sections 5.1.1 and 5.2.1 from Chapter 5, we find summary statistics:

UN_data_ch6 |> 
  select(life_exp, fert_rate, income) |> 
  tidy_summary()

column	n	group	type	min	Q1	mean	median	Q3	max	sd
life_exp	182		numeric	53.6	69.4	73.67	75.2	78.4	86.4	6.86
fert_rate	182		numeric	0.9	1.6	2.49	2.0	3.2	6.6	1.16
income	25	Low income	factor
income	52	Lower middle income	factor
income	49	Upper middle income	factor
income	56	High income	factor

Recall that each row in UN_data_ch6 represents a particular country or UN member state. The tidy_summary() function shows a summary for the numerical variables life expectancy (life_exp), fertility rate (fert_rate), and the categorical variable income group (income). When the variable is numerical, the tidy_summary() function provides the total number of observations in the data frame, the five-number summary, the mean, and the standard deviation.

For example, the first row of our summary refers to life expectancy as life_exp. There are 182 observations for this variable, it is a numerical variable, and the first quartile, Q1, is 69.4; this means that the life expectancy of 25% of the UN member states is less than 69.4 years. When a variable in the dataset is categorical, also called a factor, the summary shows all the categories or factor levels and the number of observations for each level. For example, income group (income) is a factor with four levels: Low Income, Lower middle income, Upper middle income, and High income. The summary also provides the number of states for each factor level; observe, for example, that the dataset has 56 UN member states that are considered High Income states.

Furthermore, we can compute the correlation coefficient between our two numerical variables: life_exp and fert_rate. Recall from Subsection 5.1.1 that correlation coefficients only exist between numerical variables. We observe that they are “strongly negatively” correlated.

UN_data_ch6 |> 
  get_correlation(formula = fert_rate ~ life_exp)

# A tibble: 1 × 1
     cor
   <dbl>
1 -0.815

We are ready to create data visualizations, the last of our exploratory data analysis. Given that the outcome variable fert_rate and explanatory variable life_exp are both numerical, we can create a scatterplot to display their relationship, as we did in Figure 5.2. But this time, we incorporate the categorical variable income by mapping this variable to the color aesthetic, thereby creating a colored scatterplot.

ggplot(UN_data_ch6, aes(x = life_exp, y = fert_rate, color = income)) +
  geom_point() +
  labs(x = "Life Expectancy", y = "Fertility Rate", color = "Income group") +
  geom_smooth(method = "lm", se = FALSE)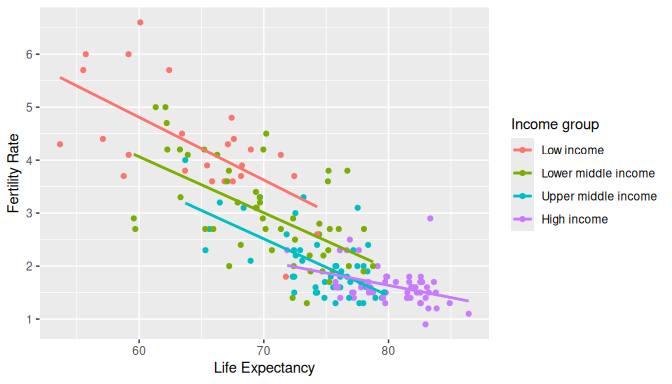

FIGURE 6.1: Colored scatterplot of life expectancy and fertility rate.

In the resulting Figure 6.1, observe that ggplot() assigns a default color scheme to the points and to the lines associated with the four levels of income: Low income, Lower middle income, Upper middle income, and High income. Furthermore, the geom_smooth(method = "lm", se = FALSE) layer automatically fits a different regression line for each group.

We can see some interesting trends. First, observe that we get a different line for each income group. Second, the slopes for all the income groups are negative. Third, the slope for the High income group is clearly less steep than the slopes for all other three groups. So, the changes in fertility rate due to changes in life expectancy are dependent on the level of income of a given country. Fourth, observe that high-income countries have, in general, high life expectancy and low fertility rates.

6.1.2 Model with interactions

We can represent the four regression lines in Figure 6.1 as a multiple regression model with interactions.

Before we do this, however, we review a linear regression with only one categorical explanatory variable. Recall in Subsection 5.2.2 we fit a regression model for each country life expectancy as a function of the corresponding continent. We produce the corresponding analysis here, now using the fertility rate as the response variable and the income group as the categorical explanatory variable. We’ll use slightly different notation to what was done previously to make the model more general.

A linear model with a categorical explanatory variable is called a one-factor model where factor refers to the categorical explanatory variable and the categories are also called factor levels. We represent the categories using indicator functions or dummy variables. In our UN data example, The variable income has four categories or levels: Low income, Lower middle income, Upper middle income, and High income. The corresponding dummy variables needed are:

\[ D_1 = \left\{ \begin{array}{ll} 1 & \text{if the UN member state has low income} \phantom{asfdasfd} \\ 0 & \text{otherwise}\end{array} \right. \] \[ D_2 = \left\{ \begin{array}{ll} 1 & \text{if the UN member state has lower middle income} \\ 0 & \text{otherwise}\end{array} \right. \] \[ D_3 = \left\{ \begin{array}{ll} 1 & \text{if the UN member state has high middle income}\phantom{a} \\ 0 & \text{otherwise}\end{array} \right. \] \[ D_4 = \left\{ \begin{array}{ll} 1 & \text{if the UN member state has high income} \phantom{asfdafd}\\ 0 & \text{otherwise}\end{array} \right.\\ \]

So, for example, if a given UN member state has Low income, its dummy variables are \(D_1 = 1\) and \(D_2 = D_3 = D_4 = 0\). Similarly, if another UN member state has High middle income, then its dummy variables would be \(D_1 = D_2 = D_4 = 0\) and \(D_3 = 1\). Using dummy variables, the mathematical formulation of the linear regression for our example is:

\[\hat y = \widehat{\text{fert rate}} = b_0 + b_2 D_2 + b_3 D_3 + b_4 D_4\]

or if we want to express it in terms of the \(i\)th observation in our dataset, we can include the \(i\)th subscript:

\[\hat y_i = \widehat{\text{fert rate}} = b_0 + b_2 D_{2i} + b_3 D_{3i} + b_4 D_{4i}\]

Recall that the coefficient \(b_0\) represents the intercept and the coefficients \(b_2\), \(b_3\), and \(b_4\) are the offsets based on the appropriate category. The dummy variables, \(D_2\), \(D_3\), and \(D_4\), take the values of zero or one depending on the corresponding category of any given country. Observe also that \(D_1\) does not appear in the model. The reason for this is entirely mathematical: if the model would contain an intercept and all the dummy variables, the model would be over-specified, that is, it would contain one redundant explanatory variable. The solution is to drop one of the variables. We keep the intercept because it provides flexibility when interpreting more complicated models, and we drop one of the dummy variables which, by default in R, is the first dummy variable, \(D_1\). This does not mean that we are losing information of the first level \(D_1\). If a country is part of the Low income level, \(D_1 = 1\), \(D_2 = D_3 = D_4 = 0\), so most of the terms in the regression are zero and the linear regression becomes:

\[\hat y = \widehat{\text{fert rate}} = b_0\] So the intercept represents the average fertility rate when the country is a Low income country. Similarly, if another country is part of the High middle income level, then \(D_1 = D_2 = D_4 = 0\) and \(D_3 = 1\) so the linear regression becomes:

\[\hat y = \widehat{\text{fert rate}} = b_0 + b_3\] The average fertility rate for a High middle income country is \(b_0 + b_3\). Observe that \(b_3\) is an offset for life expectancy between the baseline level and the High middle income level. The same logic applies to the model for each possible income category.

We calculate the regression coefficients using the lm() function and the command coef() to retrieve the coefficients of the linear regression:

one_factor_model <- lm(fert_rate ~ income, data = UN_data_ch6)
coef(one_factor_model)

We present these results on a table with the mathematical notation used above:

	Coefficients	Values
(Intercept)	b0	4.28
incomeLower middle income	b2	-1.30
incomeUpper middle income	b3	-2.25
incomeHigh income	b4	-2.65

The first level, Low income, is the “baseline” group. The average fertility rate for Low income UN member states is 4.28. Similarly, the average fertility rate for Upper middle income member states is 4.28 + -2.25 = 2.03.

We are now ready to study the multiple linear regression model with interactions shown in Figure 6.1. In this figure we can identify three different effects. First, for any fixed level of life expectancy, observe that there are four different fertility rates. They represent the effect of the categorical explanatory variable, income. Second, for any given regression line, the slope represents the change in average fertility rate due to changes on life expectancy. This is the effect of the numerical explanatory variable life_exp. Third, observe that the slope of the line depends on the income level; as an illustration, observe that for High income member states the slope is less steep than for Low income member states. When the slope changes due to changes in the explanatory variable, we call this an interaction effect.

The mathematical formulation of the linear regression model with two explanatory variables, one numerical and one categorical, and interactions is:

\[\begin{aligned}\widehat{y} = \widehat{\text{fert rate}} = b_0 &+ b_{02}D_2 + b_{03}D_3 + b_{04}D_4 \\ &+ b_1x \\ &+ b_{12}xD_2 + b_{13}xD_3 + b_{14}xD_4\end{aligned}\]

The linear regression shows how the average life expectancy is affected by the categorical variable, the numerical variable, and the interaction effects. There are eight coefficients in our model and we have separated their coefficients into three lines to highlight their different roles. The first line shows the intercept and the effects of the categorical explanatory variables. Recall that \(D_2\), \(D_3\), and \(D_4\) are the dummy variables in the model and each is equal to one or zero depending on the category of the country at hand; correspondingly, the coefficients \(b_{02}\), \(b_{03}\), and \(b_{04}\) are the offsets with respect to the baseline level of the intercept, \(b_0\). Recall that the first dummy variable has been dropped and the intercept captures this effect. The second line in the equation represents the effect of the numerical variable, \(x\). In our example \(x\) is the value of life expectancy. The coefficient \(b_1\) is the slope of the line and represents the change in fertility rate due to one unit change in life expectancy. The third line in the equation represents the interaction effects on the slopes. Observe that they are a combination of life expectancy, \(x\), and income level, \(D_2\), \(D_3\), and \(D_4\). What these interaction effects do is to modify the slope for different levels of income. For a Low income member state, the dummy variables are \(D_1 = 1\), \(D_2 = D_3 = D_4 = 0\) and our linear regression is:

\[\begin{aligned}\widehat{y} = \widehat{\text{fert rate}} &= b_0 + b_{02}\cdot 0 + b_{03}\cdot 0 + b_{04}\cdot 0 + b_1x + b_{12}x\cdot 0 + b_{13}x\cdot 0 + b_{14}x\cdot 0\\ & = b_0 + b_1x \end{aligned}\]

Similarly, for a High income member state, the dummy variables are \(D_1 = D_2 =D_3 = 0\), and \(D_4 = 1\). We take into account the offsets for the intercept, \(b_{04}\), and the slope, \(b_{14}\), and the linear regression becomes:

\[\begin{aligned}\widehat{y} = \widehat{\text{fert rate}} &= b_0 + b_{02}\cdot 0 + b_{03}\cdot 0 + b_{04}\cdot 1 + b_1 x + b_{12}x\cdot 0 + b_{13}x\cdot 0 + b_{14}x\cdot 1\\ & = b_0 + b_{04} + b_1x + b_{14}x\\ & = (b_0 + b_{04}) + (b_1 + b_{14})\cdot x\end{aligned}\]

Observe how the intercept and the slope are different for a High income member state when compared to the baseline Low income member state. As an illustration, we construct this multiple linear regression for the UN member state dataset in R. We first “fit” the model using the lm() “linear model” function and then find the coefficients using the function coef(). In R, the formula used is y ~ x1 + x2 + x1:x2 where x1 and x2 are the variable names in the dataset and represent the main effects while x1:x2 is the interaction term. For simplicity, we can also write y ~ x1 * x2 as the * sign accounts for both, main effects and interaction effects. R would let both x1 and x2 be either explanatory or numerical, and we need to make sure the dataset format is appropriate for the regression we want to run. Here is the code for our example:

# Fit regression model and get the coefficients of the model
model_int <- lm(fert_rate ~ life_exp * income, data = UN_data_ch6)
coef(model_int)

TABLE 6.2: Regression table for interaction model

	Coefficients	Values
(Intercept)	b0	11.918
incomeLower middle income	b02	-1.504
incomeUpper middle income	b03	-1.893
incomeHigh income	b04	-6.580
life_exp	b1	-0.118
incomeLower middle income:life_exp	b12	0.013
incomeUpper middle income:life_exp	b13	0.011
incomeHigh income:life_exp	b14	0.072

We can match the coefficients with the values computed in Table 6.2: the fitted fertility rate \(\widehat{y} = \widehat{\text{fert rate}}\) for Low income countries is

\[\widehat{\text{fert rate}} = b_0 + b_1\cdot x = 11.92 + (-0.12)\cdot x,\]

which is the equation of the regression line in Figure 6.1 for low income countries. The regression has an intercept of 11.92 and a slope of -0.12. Since life expectancy is greater than zero for all countries, the intercept has no practical interpretation and we only need it to produce the most appropriate line. The interpretation of the slope is: for Low income countries, every additional year of life expectancy reduces the average fertility rate by 0.12 units.

As discussed earlier, the intercept and slope for all the other income groups are determined by taking into account the appropriate offsets. For example, for High income countries \(D_4 = 1\) and all other dummy variables are equal to zero. The regression line becomes

\[\widehat{y} = \widehat{\text{fert rate}} = b_0 + b_1x + b_{04} + b_{14}x = (b_0 + b_{04} ) + (b_1+b_{14})x \]

where \(x\) is life expectancy, life_exp. The intercept is (Intercept) + incomeHigh income:

\[b_0 + b_{04} = 11.92 +(-6.58) = 5.34,\]

and the slope for these High income countries is life_exp + life_exp:incomeHigh income corresponding to

\[b_1 + b_{14}= -0.12 + 0.07 = -0.05.\]

For High income countries, every additional year of life expectancy reduces the average fertility rate by 0.05 units. The intercepts and slopes for other income levels are calculated similarly.

Since the life expectancy for Low income countries has a steeper slope than High income countries, one additional year of life expectancy will decrease fertility rates more for the low-income group than for the high-income group. This is consistent with our observation from Figure 6.1. When the associated effect of one variable depends on the value of another variable we say that there is an interaction effect. This is the reason why the regression slopes are different for different income groups.

Learning check

(LC6.1) What is the goal of including an interaction term in a multiple regression model?

• A. To create more variables for analysis.
• B. To account for the effect of one explanatory variable on the response while considering the influence of another explanatory variable.
• C. To make the model more complex without any real benefit.
• D. To automatically improve the fit of the regression line.

(LC6.2) How does the inclusion of both main effects and interaction terms in a regression model affect the interpretation of individual coefficients?

• A. They represent simple marginal effects.
• B. They become meaningless.
• C. They are conditional effects, depending on the level of the interacting variables.
• D. They are interpreted in the same way as in models without interactions.

(LC6.3) Which statement about the use of dummy variables in regression models is correct?

• A. Dummy variables are used to represent numerical variables.
• B. Dummy variables are used to represent categorical variables at least two levels.
• C. Dummy variables always decrease the R-squared value.
• D. Dummy variables are unnecessary in regression models.

6.1.3 Model without interactions

We can simplify the previous model by removing the interaction effects. The model still represents different income groups with different regression lines by allowing different intercepts but all the lines have the same slope: they are parallel as shown in Figure 6.2.

To plot parallel slopes we use the function geom_parallel_slopes() that is included in the moderndive package. To use this function you need to load both the ggplot2 and moderndive packages. Observe how the code is identical to the one used for the model with interactions in Figure 6.1, but now the geom_smooth(method = "lm", se = FALSE) layer is replaced with geom_parallel_slopes(se = FALSE).

ggplot(UN_data_ch6, aes(x = life_exp, y = fert_rate, color = income)) +
  geom_point() +
  labs(x = "Life expectancy", y = "Fertility rate", color = "Income group") +
  geom_parallel_slopes(se = FALSE)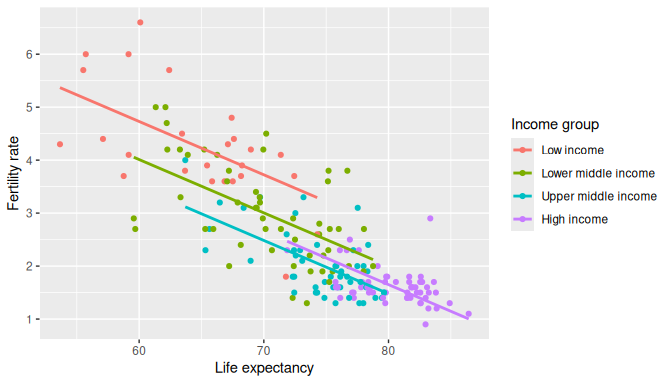

FIGURE 6.2: Parallel slopes model of fertility rate with life expectancy and income.

The regression lines for each income group are shown in Figure 6.2. Observe that the lines are now parallel: they all have the same negative slope. The interpretation of this result is that the change in fertility rate due to changes in life expectancy in a given country are the same regardless the income group of this country.

On the other hand, any two regression lines in Figure 6.2 have different intercepts representing the income group; in particular, observe that for any fixed level of life expectancy the fertility rate is greater for Low income and Lower middle income countries than for Upper middle income and High income countries.

The mathematical formulation of the linear regression model with two explanatory variables, one numerical and one categorical, and without interactions is:

\[\widehat{y} = b_0 + b_{02}D_2 + b_{03}D_3 + b_{04}D_4+ b_1x.\] Observe that the dummy variables only affect the intercept now, and the slope is fully described by \(b_1\) for any income group. In the UN data example, a High income country, with \(D_4 = 1\) and the other dummy variables equal to zero, will be represented by

\[\widehat{y} = (b_0 + b_{04})+ b_1x.\]

To find the coefficients for this regression in R, the formula used is y ~ x1 + x2 where x1 and x2 are the variable names in the dataset and represent the main effects. Observe that the term x1:x2 representing the interaction is no longer included. R would let both x1 and x2 to be either explanatory or numerical; therefore, we should always check that the variable format is appropriate for the regression we want to run. Here is the code for the UN data example:

# Fit regression model:
model_no_int <- lm(fert_rate ~ life_exp + income, data = UN_data_ch6)

# Get the coefficients of the model
coef(model_no_int)

TABLE 6.3: Regression table for a model without interactions

	Coefficients	Values
(Intercept)	b0	10.768
incomeLower middle income	b02	-0.719
incomeUpper middle income	b03	-1.239
incomeHigh income	b04	-1.067
life_exp	b1	-0.101

In this model without interactions presented in Table 6.3, the slope is the same for all the regression lines, \(b_1 = -0.101\). Assuming that this model is correct, for any UN member state, every additional year of life expectancy reduces the average fertility rate by 0.101 units, regardless of the income level of the member state. The intercept of the regression line for Low income member states is 10.768 while for High income member states is \(10.768 + (-1.067) = 9.701\). The intercepts for other income levels can be determined similarly. We compare the visualizations for both models side-by-side in Figure 6.3.

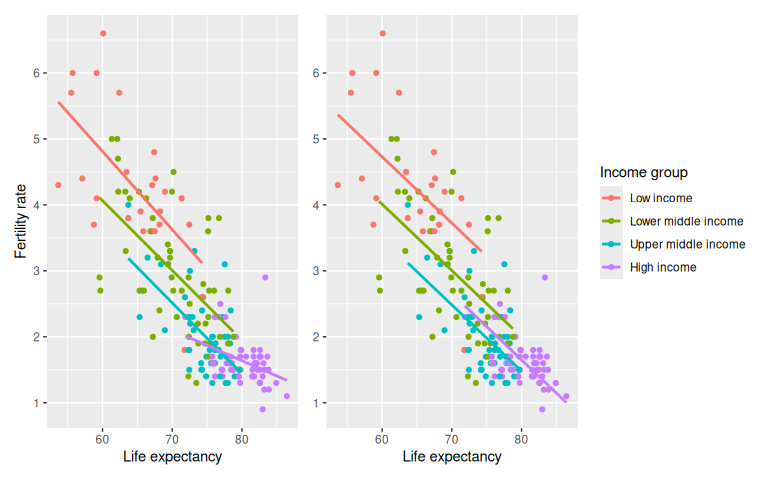
FIGURE 6.3: Comparison of interaction and parallel slopes models.

Which one is the preferred model? Looking at the scatterplot and the clusters of points in Figure 6.3, it does appear that lines with different slopes capture better the behavior of different groups of points. The lines do not appear to be parallel and the interaction model seems more appropriate.

Learning check

(LC6.4) How should a model with one categorical regressor and one numerical regressor, but no interactions, be interpreted?

• A. The slope of the model for each category is different.
• B. The slope of the model for each category is the same.
• C. There is no relationship between the categorical regressor and the response.
• D. There is no relationship between the numerical regressor and the response.

6.1.4 Observed responses, fitted values, and residuals

In this subsection, we work with the regression model with interactions. The coefficients for this model were found earlier, saved in model_int, and are displayed in Table 6.4:

TABLE 6.4: Regression table for interaction model

	Coefficients	Values
(Intercept)	b0	11.918
incomeLower middle income	b02	-1.504
incomeUpper middle income	b03	-1.893
incomeHigh income	b04	-6.580
life_exp	b1	-0.118
incomeLower middle income:life_exp	b12	0.013
incomeUpper middle income:life_exp	b13	0.011
incomeHigh income:life_exp	b14	0.072

We can use these coefficients to find the fitted values and residuals for any given observation. As an illustration, we chose two observations from the UN member states dataset, provided the values for the explanatory variables and response, as well as the fitted values and residuals:

ID	fert_rate	income	life_exp	fert_rate_hat	residual
1	1.3	High income	79.7	1.65	-0.35
2	5.7	Low income	62.4	4.52	1.18

The first observation is a High income country with a life expectancy of 79.74 years and an observed fertility rate equal to 1.3. The second observation is a Low income country with a life expectancy of 62.41 years and an observed fertility rate equal to 5.7 The fitted value, \(\hat y\), called fert_rate_hat in the table, is the estimated value of the response determined by the regression line. This value is computed by using the values of the explanatory variables and the coefficients of the linear regression. In addition, recall the difference between the observed response value and the fitted value, \(y - \hat y\), is called the residual.

We illustrate this in Figure 6.4. The vertical line on the left represents the life expectancy value for the Low income country. The y-value for the large dot on the regression line that intersects the vertical line is the fitted value for fertility rate, \(\widehat y\), and the y-value for the large dot above the line is the observed fertility rate, \(y\). The difference between these values, \(y - \widehat y\), is called the residual and in this case is positive. Similarly, the vertical line on the right represents the life expectancy value for the High income country, the y-value for the large dot on the regression line is the fitted fertility rate. The observed y-value for fertility rate is below the regression line making the residual negative.

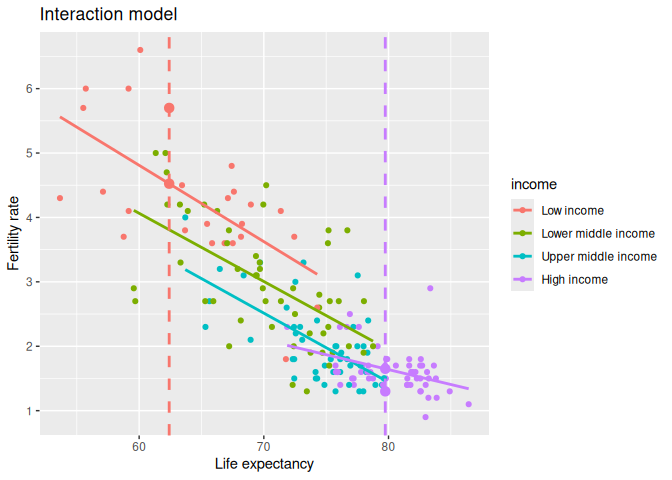
FIGURE 6.4: Fitted values for two new countries.

We can generalize the study of fitted values and residuals for all the countries in the UN_data_ch6 dataset, as shown in Table 6.5.

regression_points <- get_regression_points(model_int)
regression_points

TABLE 6.5: Regression points (First 10 out of 182 countries)

ID	fert_rate	income	life_exp	fert_rate_hat	residual
1	4.3	Low income	53.6	5.56	-1.262
2	1.4	Upper middle income	79.5	1.50	-0.098
3	2.7	Lower middle income	78.0	2.16	0.544
4	5.0	Lower middle income	62.1	3.84	1.159
5	1.6	High income	77.8	1.74	-0.139
6	1.9	Upper middle income	78.3	1.62	0.278
7	1.6	Upper middle income	76.1	1.86	-0.256
8	1.6	High income	83.1	1.50	0.105
9	1.5	High income	82.3	1.53	-0.033
10	1.6	Upper middle income	74.2	2.07	-0.469

Learning check

(LC6.5) Compute the observed response values, fitted values, and residuals for the model without interactions.

(LC6.6) What is the main benefit of visualizing the fitted values and residuals of a multiple regression model?

• A. To find errors in the dataset.
• B. To check the assumptions of the regression model, such as linearity and homoscedasticity.
• C. To always improve the model’s accuracy.
• D. To increase the complexity of the model.

6.2 Two numerical explanatory variables

We now consider regression models with two numerical explanatory variables. To illustrate this situation we explore the ISLR2 R package for the first time in this book using its Credit dataset. This dataset contains simulated information for 400 customers. For the regression model we use the credit card balance (Balance) as the response variable; and the credit limit (Limit), and the income (Income) as the numerical explanatory variables.

6.2.1 Exploratory data analysis

We load the Credit data frame and to ensure the type of behavior we have become accustomed to in using the tidyverse, we also convert this data frame to be a tibble using as_tibble(). We construct a new data frame credit_ch6 with only the variables needed. We do this by using the select() verb as we did in Subsection 3.8.1 and, in addition, we save the selecting variables with different names: Balance becomes debt, Limit becomes credit_limit, and Income becomes income:

library(ISLR2)
credit_ch6 <- Credit |> as_tibble() |> 
  select(debt = Balance, credit_limit = Limit, 
         income = Income, credit_rating = Rating, age = Age)

You can observe the effect of our use of select() by looking at the raw values either in RStudio’s spreadsheet viewer or by using glimpse().

glimpse(credit_ch6)

Rows: 400
Columns: 5
$ debt          <dbl> 333, 903, 580, 964, 331, 1151, 203, 872, 279, 1350, 1407, 0, 204, 1081, 148, 0, 0, 368, 891, 104…
$ credit_limit  <dbl> 3606, 6645, 7075, 9504, 4897, 8047, 3388, 7114, 3300, 6819, 8117, 1311, 5308, 6922, 3291, 2525, …
$ income        <dbl> 14.9, 106.0, 104.6, 148.9, 55.9, 80.2, 21.0, 71.4, 15.1, 71.1, 63.1, 15.0, 80.6, 43.7, 19.1, 20.…
$ credit_rating <dbl> 283, 483, 514, 681, 357, 569, 259, 512, 266, 491, 589, 138, 394, 511, 269, 200, 286, 339, 448, 4…
$ age           <dbl> 34, 82, 71, 36, 68, 77, 37, 87, 66, 41, 30, 64, 57, 49, 75, 57, 73, 69, 28, 44, 63, 72, 61, 48, …

Furthermore, we present a random sample of five out of the 400 credit card holders in Table 6.6. As observed before, each time you run this code, a different subset of five rows is given.

credit_ch6 |> sample_n(size = 5)

TABLE 6.6: Random sample of 5 credit card holders

debt	credit_limit	income	credit_rating	age
0	1402	27.2	128	67
1081	6922	43.7	511	49
1237	7499	58.0	560	67
379	4742	57.1	372	79
1151	8047	80.2	569	77

Note that income is in thousands of dollars while debt and credit limit are in dollars. We can also compute summary statistics using the tidy_summary() function. We only select() the columns of interest for our model as shown in Table 6.7:

credit_ch6 |> select(debt, credit_limit, income) |> tidy_summary()

TABLE 6.7: Summary of credit data

column	n	group	type	min	Q1	mean	median	Q3	max	sd
debt	400		numeric	0.0	68.8	520.0	459.5	863.0	1999	459.8
credit_limit	400		numeric	855.0	3088.0	4735.6	4622.5	5872.8	13913	2308.2
income	400		numeric	10.4	21.0	45.2	33.1	57.5	187	35.2

The mean and median credit card debt are $520.0 and $459.5, respectively. The first quartile for debt is 68.8; this means that 25% of card holders had debts of $68.80 or less. Correspondingly, the mean and median credit card limit, credit_limit, are around $4,736 and $4,622, respectively. Note also that the third quartile of income is 57.5; so 75% of card holders had incomes below $57,500.

We visualize the relationship of the response variable with each of the two explanatory variables using this R code. These plots are shown in Figure 6.5.

ggplot(credit_ch6, aes(x = credit_limit, y = debt)) +
  geom_point() +
  labs(x = "Credit limit (in $)", y = "Credit card debt (in $)", 
       title = "Debt and credit limit") +
  geom_smooth(method = "lm", se = FALSE)

ggplot(credit_ch6, aes(x = income, y = debt)) +
  geom_point() +
  labs(x = "Income (in $1000)", y = "Credit card debt (in $)", 
       title = "Debt and income") +
  geom_smooth(method = "lm", se = FALSE)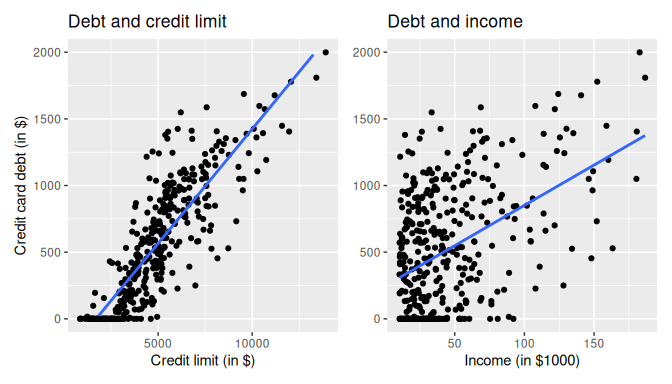

FIGURE 6.5: Relationship between credit card debt and credit limit/income.

The left plot in Figure 6.5 shows a positive and linear association between credit limit and credit card debt: as credit limit increases so does credit card debt. Observe also that many customers have no credit card debt and there is a cluster of points at the credit card debt value of zero. The right plot in Figure 6.5 shows also positive and somewhat linear association between income and credit card debt, but this association seems weaker and actually appears positive only for incomes larger than $50,000. For lower income values it is not clear there is any association at all.

Since variables debt, credit_limit, and income are numerical, and more importantly, the associations between the response and explanatory variables appear to be linear or close to linear, we can also calculate the correlation coefficient between any two of these variables. Recall that the correlation coefficient is appropriate if the association between the variables is linear. One way to do this is using the get_correlation() command as seen in Subsection 5.1.1, once for each explanatory variable with the response debt:

credit_ch6 |> get_correlation(debt ~ credit_limit)
credit_ch6 |> get_correlation(debt ~ income)

Alternatively, using the select() verb and command cor() we can find all correlations simultaneously by returning a correlation matrix as shown in Table 6.8. This matrix shows the correlation coefficient for any pair of variables in the appropriate row/column combination.

credit_ch6 |> select(debt, credit_limit, income) |> cor()

TABLE 6.8: Correlation coefficients between credit card debt, credit limit, and income

	debt	credit_limit	income
debt	1.000	0.862	0.464
credit_limit	0.862	1.000	0.792
income	0.464	0.792	1.000

Let’s look at some findings presented in the correlation matrix:

1. The diagonal values are all 1 because, based on the definition of the correlation coefficient, the correlation of a variable with itself is always 1.
2. The correlation between debt and credit_limit is 0.862. This indicates a strong and positive linear relationship: the greater the credit limit is, the larger is the credit card debt, on average.
3. The correlation between debt and income is 0.464. The linear relationship is positive albeit somewhat weak. In other words, higher income is only weakly associated with higher debt.
4. Observe also that the correlation coefficient between the two explanatory variables, credit_limit and income, is 0.792.

A useful property of the correlation coefficient is that it is invariant to linear transformations; this means that the correlation between two variables, \(x\) and \(y\), will be the same as the correlation between \((a\cdot x + b)\) and \(y\) for any constants \(a\) and \(b\). To illustrate this, observe that the correlation coefficient between income in thousands of dollars and credit card debt was 0.464. If we now find the correlation income in dollars, by multiplying income by 1000, and credit card debt we get:

credit_ch6 |> get_correlation(debt ~ 1000 * income)

# A tibble: 1 × 1
    cor
  <dbl>
1 0.464

The correlation is exactly the same.

We return to our exploratory data analysis of the multiple regression. The plots in Figure 6.5 correspond to the response and each of the explanatory variables separately. In Figure 6.6 we show a 3-dimensional (3D) scatterplot representing the joint relationship of all three variables simultaneously. Each of the 400 observations in the credit_ch6 data frame are marked with a blue point where

1. The response variable \(y\), debt, is on the vertical axis.
2. The regressors \(x_1\), income, and \(x_2\), credit_limit, are on the two axes that form the bottom plane.

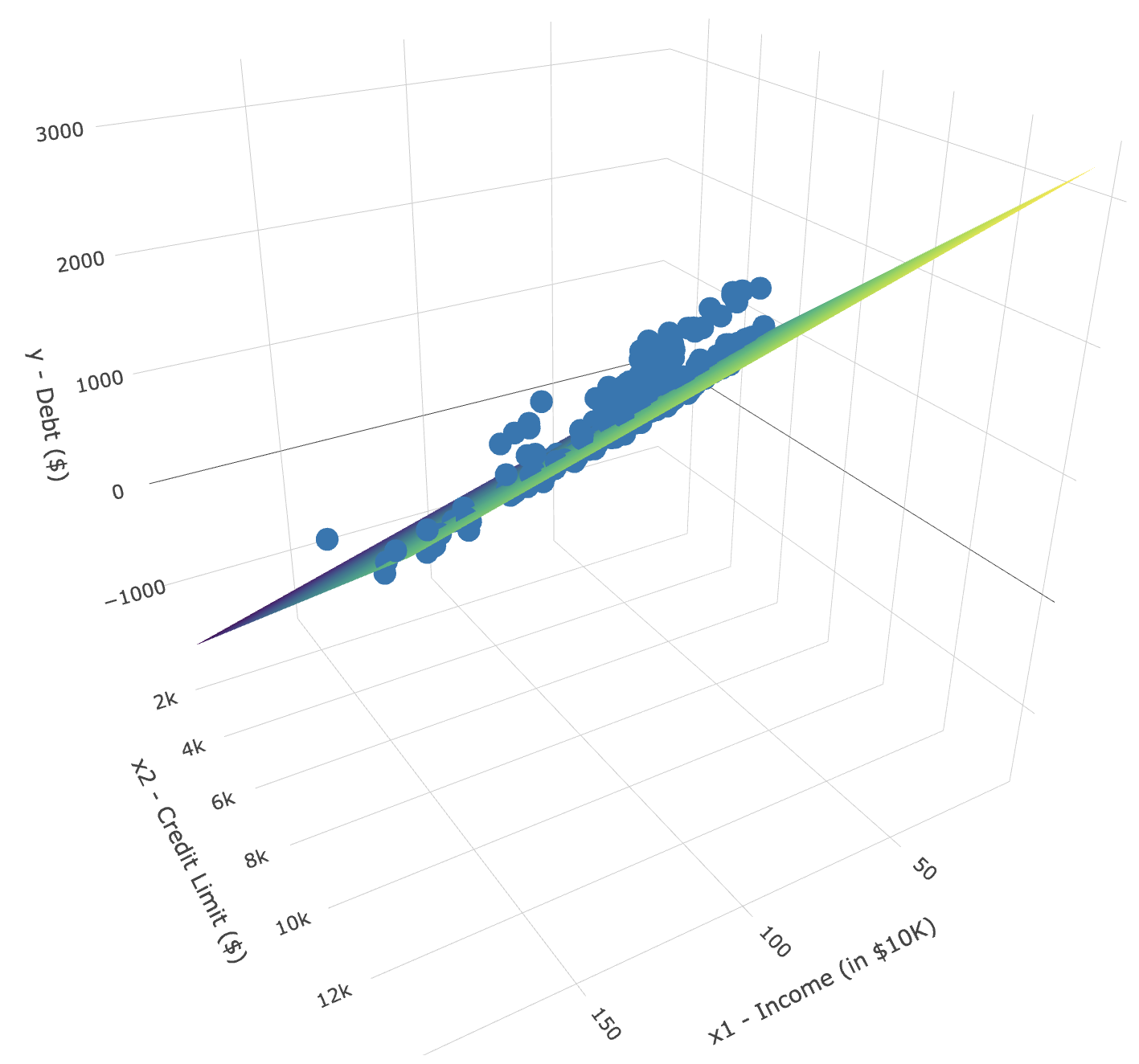
FIGURE 6.6: 3D scatterplot and regression plane.

In addition, Figure 6.6 includes a regression plane. Recall from Subsection 5.3.2 that the linear regression with one numerical explanatory variable selects the “best-fitting” line: the line that minimizes the sum of squared residuals. When linear regression is performed with two numerical explanatory variables, the solution is a “best-fitting” plane: the plane that minimizes the sum of squared residuals. Visit this website to open an interactive version of this plot in your browser.

Learning check

(LC6.7) Conduct a new exploratory data analysis with the same outcome variable \(y\) debt but with credit_rating and age as the new explanatory variables \(x_1\) and \(x_2\). What can you say about the relationship between a credit card holder’s debt and their credit rating and age?

6.2.2 Multiple regression with two numerical regressors

As shown in Figure 6.6, the linear regression with two numerical regressors produces the “best-fitting” plane. We start with a model with no interactions for the two numerical explanatory variables income and credit_limit. In R we consider a model fit with a formula of the form y ~ x1 + x2. We retrieve the regression coefficients using the lm() function and the command coef() to get the coefficients of the linear regression. The regression coefficients are shown in what follows.

debt_model <- lm(debt ~ credit_limit + income, data = credit_ch6)
coef(debt_model)

We present these results in a table with the mathematical notation used above:

	Coefficients	Values
(Intercept)	b0	-385.179
credit_limit	b1	0.264
income	b2	-7.663

1. We determine the linear regression coefficients using lm(y ~ x1 + x2, data) where x1 and x2 are the two numerical explanatory variables used.
2. We extract the coefficients from the output using the coef() command.

Let’s interpret the coefficients. The intercept value is -$385.179. If the range of values that the regressors could take include a credit_limit of $0 and an income of $0, the intercept would represent the average credit card debt for an individual with those levels of credit_limit and income. This is not the case in our data and the intercept has no practical interpretation; it is mainly used to determine where the plane should cut the \(y\)-intercept to produce the smallest sum of squared residuals.

Each slope in a multiple linear regression is considered a partial slope and represents the marginal or additional contribution of a regressor when it is added to a model that already contains other regressors. This partial slope is typically different than the slope we may find in a simple linear regression for the same regressor. The reason is that, typically, regressors are correlated, so when one regressor is part of a model, indirectly it’s also explaining part of the other regressor. When the second regressor is added to the model, it helps explain only changes in the response that were not already accounted for by the first regressor. For example, the slope for credit_limit is $0.264. Keeping income fixed to some value, for an additional increase of credit limit by one dollar the credit debt increases, on average, by $0.264. Similarly, the slope of income is -$7.663. Keeping credit_limit fixed to some level, for a one unit increase of income ($1000 in actual income), there is an associated decrease of $7.66 in credit card debt, on average.

Putting these results together, the equation of the regression plane that gives us fitted values \(\widehat{y}\) = \(\widehat{\text{debt}}\) is:

\[ \begin{aligned} \widehat{y} = \widehat{\text{debt}} &= b_0 + b_1 \cdot x_1 + b_2 \cdot x_2\\ &= -385.179 + 0.263 \cdot x_1 - 7.663 \cdot x_2 \end{aligned} \] where \(x_1\) represents credit limit and \(x_2\) income.

To illustrate the role of partial slopes further, observe that the right plot in Figure 6.5 shows the relationship between debt and income in isolation, a positive relationship, so the slope of income is positive. We can determine the value of this slope by constructing a simple linear regression using income as the only regressor:

# Fit regression model and get the coefficients of the model
simple_model <- lm(debt ~ income, data = credit_ch6)
coef(simple_model)

	Coefficients	Values
(Intercept)	b0’	246.51
income	b2’	6.05

The regression line is given by the following with the coefficients denoted using the prime (\('\)) designation since they are different values than what we saw previously

\[ \begin{aligned} \widehat{y} = \widehat{\text{debt}} &= b_0' + b_2' \cdot x_2 = 246.515 + 6.048 \cdot x_2 \end{aligned} \] where \(x_2\) is income. By contrast, when credit_limit and income are considered jointly to explain changes in debt, the equation for the multiple linear regression was:

\[ \begin{aligned} \widehat{y} = \widehat{\text{debt}} &= b_0 + b_1 \cdot x_1 + b_2 \cdot x_2\\ &= -385.179 + 0.263 \cdot x_1 - 7.663 \cdot x_2 \end{aligned} \]

So the slope for income in a simple linear regression is 6.048, and the slope for income in a multiple linear regression is \(-7.663\). As surprising as these results may appear at first, they are perfectly valid and consistent as the slope of a simple linear regression has a different role than the partial slope of a multiple linear regression. The latter is the additional effect of income on debt when credit_limit has already been taken into account.

Learning check

(LC6.8) Fit a new simple linear regression using lm(debt ~ credit_rating + age, data = credit_ch6) where credit_rating and age are the new numerical explanatory variables \(x_1\) and \(x_2\). Get information about the “best-fitting” regression plane from the regression table by finding the coefficient of the model. How do the regression results match up with the results from your previous exploratory data analysis?

(LC6.9) Which of the following statements best describes the interpretation of a regression coefficient in a multiple regression model?

• A. It is the additional effect of a regressor on the response when other regressors have already been taken into account.
• B. It is the average response variable value when all explanatory variables are zero.
• C. It is always positive if the correlation is strong.
• D. It cannot be interpreted if there are more than two explanatory variables.

(LC6.10) What is a characteristic of the “best-fitting” plane in a multiple regression model with two numerical explanatory variables?

• A. It represents the line of best fit for each explanatory variable separately.
• B. It minimizes the product of residuals.
• C. It minimizes the sum of squared residuals for all combinations of regressors.
• D. It shows the exact predictions for every data point.

(LC6.11) What does the intercept represent in a multiple regression model with two explanatory variables?

• A. The effect of one explanatory variable, keeping the other constant.
• B. The change in the response variable per unit change in the explanatory variable.
• C. The correlation between the two explanatory variables.
• D. The expected value of the response variable when all regressors are zero.

(LC6.12) What does the term “partial slope” refer to in a multiple regression model?

• A. The additional effect of a regressor on the response variable, when all the other regressors have been taken into account.
• B. The total slope of all variables combined.
• C. The slope when all variables are zero.
• D. The average of all slopes in the model.

6.2.3 Observed/fitted values and residuals

As shown in Subsection 6.1.4 for the UN member states example, we find the fitted values and residuals for our credit card debt regression model. The fitted values for the credit card debt (\(\widehat{\text{debt}}\)) are computed using the equation for the regression plane:

\[ \begin{aligned} \widehat{y} = \widehat{\text{debt}} &= -385.179 + 0.263 \cdot x_1 - 7.663 \cdot x_2 \end{aligned} \] where \(x_1\) is credit_limit and \(x_2\) is income. The residuals are the difference between the observed credit card debt and the fitted credit card debt, \(y - \widehat y\), for each observation in the data set. In R, we find the fitted values, debt_hat, and residuals, residual, using the get_regression_points() function. In Table 6.9 we present the first 10 rows of output. Remember that the coordinates of each of the points in our 3D scatterplot in Figure 6.6 can be found in the income, credit_limit, and debt columns.

get_regression_points(debt_model)

TABLE 6.9: Regression points (First 10 credit card holders out of 400)

ID	debt	credit_limit	income	debt_hat	residual
1	333	3606	14.9	454	-120.8
2	903	6645	106.0	559	344.3
3	580	7075	104.6	683	-103.4
4	964	9504	148.9	986	-21.7
5	331	4897	55.9	481	-150.0
6	1151	8047	80.2	1127	23.6
7	203	3388	21.0	349	-146.4
8	872	7114	71.4	948	-76.0
9	279	3300	15.1	371	-92.2
10	1350	6819	71.1	873	477.3

6.3 Conclusion

6.3.1 Additional resources

An R script file of all R code used in this chapter is available here.

6.3.2 What’s to come?

This chapter concludes the “Statistical/Data Modeling with moderndive” portion of this book. We are ready to proceed to Part III: “Statistical Inference with infer.” Statistical inference is the science of inferring about some unknown quantity using sampling. So far, we have only studied the regression coefficients and their interpretation. In later chapters we learn how we can use information from a sample to make inferences about the entire population.

Once we have covered Chapters 7 on sampling, 8 on confidence intervals, and 9 on hypothesis testing, we revisit the regression models in Chapter 10 on inference for regression. This will complete the topics in this book, as shown in Figure 6.7!

Also in Chapter 10, we revisit the concept of residuals \(y - \widehat{y}\) and discuss their importance when interpreting the results of a regression model. We perform what is known as a residual analysis of the residual variable of all get_regression_points() outputs. Residual analyses enable us to verify what are known as the conditions for inference for regression.

FIGURE 6.7: ModernDive flowchart – on to Part III!