9 Hypothesis Testing

We have studied confidence intervals in Chapter 8. We now introduce hypothesis testing, another widely used method for statistical inference. A claim is made about a value or characteristic of the population and then a random sample is used to infer about the plausibility of this claim or hypothesis. For example, in Section 9.2, we use data collected from Spotify to investigate whether metal music is more popular than deep-house music.

Many of the relevant concepts, ideas, and we have already introduced many of the necessary concepts to understand hypothesis testing in Chapters 7 and 8. We can now expand further on these ideas and provide a general framework for understanding hypothesis tests. By understanding this general framework, you will be able to adapt it to many different scenarios.

The same can be said for confidence intervals. There was one general framework that applies to confidence intervals, and the infer package was designed around this framework. While the specifics may change slightly for different types of confidence intervals, the general framework stays the same.

We believe that this approach is better for long-term learning than focusing on specific details for specific confidence intervals. We prefer this approach also for hypothesis tests as well, but we will tie the ideas into the traditional theory-based methods as well for completeness.

In Section 9.1 we review confidence intervals and introduce hypothesis tests for one-sample problems; in particular, for the mean $\mu$. We use both theory-based and simulation-based approaches, and we provide some justification why we consider it a better idea to carefully unpack the simulation-based approach for hypothesis testing in the context of two-sample problems. We also show the direct link between confidence intervals and hypothesis tests. In Section 9.2 we introduce the activity that motivates the simulation-based approach for two-sample problems, data collected from Spotify to investigate whether metal music is more popular than deep-house music. In Sections 9.3, 9.4, and 9.5 we explain, conduct, and interpret hypothesis tests, respectively, using the simulation-based approach of permutation. We introduce a case study in Section 9.6, and in Section 9.7 we conclude with a discussion of the theory-based approach for two-sample problems and some additional remarks.

If you’d like more practice or you are curious to see how this framework applies to different scenarios, you can find fully-worked out examples for many common hypothesis tests and their corresponding confidence intervals in the Appendices online.We recommend that you carefully review these examples as they also cover how the general frameworks apply to traditional theory-based methods like the $t$-test and normal-theory confidence intervals. You will see there that these traditional methods are just approximations for the computer-based methods we have been focusing on. However, they also require conditions to be met for their results to be valid. Computer-based methods using randomization, simulation, and bootstrapping have much fewer restrictions. Furthermore, they help develop your computational thinking, which is one big reason they are emphasized throughout this book.

Needed packages

If needed, read Section 1.3 for information on how to install and load R packages.

library(tidyverse)
library(moderndive)
library(infer)
library(nycflights23)
library(ggplot2movies)

Recall that loading the tidyverse package loads many packages that we have encountered earlier. For details refer to Section 4.4. The packages moderndive and infer contain functions and data frames that will be used in this chapter.

9.1 Tying confidence intervals to hypothesis testing

In Chapter 8, we used a random sample to construct an interval estimate of the population mean. When using the theory-based approach, we relied on the Central Limit Theorem to form these intervals and when using the simulation-based approach we do it, for example, using the bootstrap percentile method. Hypothesis testing takes advantages of similar tools but the nature and the goal of the problem are different. Still, there is a direct link between confidence intervals and hypothesis testing.

In this section, we first describe the one-sample hypothesis test for the population mean. We then establish the connection between confidence intervals and hypothesis test. This connection is direct when using the theory-based approach but requires careful consideration when using the simulation-based approach.

We proceed by describing hypothesis testing in the case of two-sample problems.

9.1.1 The one-sample hypothesis test for the population mean

Let’s continue working with the population mean, $\mu$. In Chapter 8, we used a random sample to construct a 95% confidence interval for $\mu$.

When performing hypothesis testing, we test a claim about $\mu$ by collecting a random sample and using it to determine if the sample obtained is consistent with the claim made. To illustrate this idea we return to the chocolate-covered almonds activity. Assume that the almonds’ company has stated on its website that the average weight of a chocolate-covered almond is exactly 3.6 grams. We are not so sure about this claim and as researchers believe that it is different than 3.6 grams on average. To test these competing claims, we again use the random sample almonds_sample_100 from the moderndive package, and the first 10 lines are shown:

almonds_sample_100

# A tibble: 100 × 2
      ID weight
   <int>  <dbl>
 1   166    4.2
 2  1215    4.2
 3  1899    3.9
 4  1912    3.8
 5  4637    3.3
 6   511    3.5
 7   127    4  
 8  4419    3.5
 9  4729    4.2
10  2574    4.1
# ℹ 90 more rows

The goal of hypothesis testing is to answer the question: “Assuming that this claim is true, how likely is it to observe a sample as extreme as or more extreme than the one we have observed?” When the answer to the question is: “If the claim was true, it would be very unlikely to observe a sample such as the one we have obtained” we would conclude that the claim cannot be true and we would reject it. Otherwise, we would fail to reject the claim.

The claim is a statement called the null hypothesis, $H_0$. It is a statement about $\mu$, and it is initially assumed to be true. A competing statement called the alternative hypothesis, $H_A$, is also a statement about $\mu$ and contains all the possible values not included under the null hypothesis. In the almonds’ activity the hypotheses are:

\[\begin{aligned} &H_0: &\mu = 3.6\\ &H_A: &\mu \ne 3.6 \end{aligned}\]

Evidence against the null may appear if the estimate of $\mu$ in the random sample collected, the sample mean, is much greater or much less than the value of $\mu$ under the null hypothesis.

How do we determine which claim should be the null hypothesis and which one the alternative hypothesis? Always remember that the null hypothesis has a privileged status since we assume it to be true until we find evidence against it. We only rule in favor of the alternative hypothesis if we find evidence in the data to reject the null hypothesis. In this context, a researcher who wants to show some results or conclusions for new findings, needs to prove that the null hypothesis is not true by finding evidence against it. We often say that the researcher bears the burden of proof.

The hypothesis shown above represents a two-sided test because evidence against the null hypothesis could come from either direction (greater or less). Sometimes it is convenient to work with a left-sided test. In our example, the claim under the null hypothesis becomes: “the average weight is at least 3.6 grams” and the researcher’s goal is to find evidence against this claim in favor of the competing claim “the weight is less than 3.6 grams.” The competing hypotheses can now be written as $H_0: \mu \ge 3.6$ versus $H_A: \mu < 3.6$ or even as $H_0: \mu = 3.6$ versus $H_A: \mu < 3.6$. Notice that we can drop the inequality part from the null hypothesis. We find this simplification convenient as we focus on the equal part of the null hypothesis only and becomes clearer that evidence against the null hypothesis may come only with values to the left of 3.6, hence a left-sided test.

Similarly, a right-sided test can be stated $H_0: \mu = 3.6$ versus $H_A: \mu > 3.6$. Claims under the null hypothesis for this type of test could be stated as “the average weight is at most 3.6 grams” or even “the average weight is less than 3.6 grams.” But observe that less does not contain the equal part, how can the null then be $H_0: \mu = 3.6$? The reason is related to the method used more than the semantics of the statement. Let’s break this down: If, under the null hypothesis, the average weight is less than 3.6 grams, we can only find evidence against the null if we find sample means that are much greater than 3.6 grams, hence the alternative hypothesis is $H_A: \mu > 3.6$. Now, to find the evidence we are looking for, the methods we use require a point of reference, “less than 3.6” is not a fixed number since 2 is less than 3.6 but so too is 3.59. On the other hand, if we can find evidence that the average is greater than 3.6, then it is also true that the average is greater than 3.5, 2, or any other number less than 3.6. Thus, as a convention, we include the equal sign always in the statement under the null hypothesis.

Let’s return to the test. We work with the two-sided test in what follows, but we will comment about the changes needed in the process if we are instead working with the left- or right-sided alternatives.

The theory-based approach

We use the theory-based approach to illustrate how a hypothesis test is conducted. We first calculate the sample mean and sample standard deviation from this sample:

almonds_sample_100 |>
  summarize(sample_mean = mean(weight),
            sample_sd = sd(weight))

# A tibble: 1 × 2
  sample_mean sample_sd
        <dbl>     <dbl>
1       3.682  0.362199

We recall that due to the Central Limit Theorem described in Subsection 7.3, the sample mean weight of almonds, $\overline X$, is approximately normally distributed with expected value equal to $\mu$ and standard deviation equal to $\sigma/\sqrt{n}$. Since the population standard deviation is unknown, we use the sample standard deviation, $s$, to calculate the standard error $s/\sqrt{n}$. As presented in Subsection 8.1.4, the $t$-test statistic

\[t = \frac{\overline{x} - \mu}{s/\sqrt{n}}\] follows a $t$ distribution with $n-1$ degrees of freedom. Of course, we do not know what $\mu$ is. But since we assume that the null hypothesis is true, we can use this value to obtain the test statistic as shown in this code next. Table 9.1 presents these values.

almonds_sample_100 |>
  summarize(x_bar = mean(weight),
            s = sd(weight),
            n = length(weight),
            t = (x_bar - 3.6)/(s/sqrt(n)))

TABLE 9.1: Sample mean, standard deviation, size, and the t-test statistic
x_bar	s	n	t
3.68	0.362	100	2.26

The value of $t = 2.26$ is the sample mean standardized such that the claim $\mu = 3.6$ grams corresponds to the center of the $t$ distribution ($t = 0$), and the sample mean observed, $\overline x = 0.36$, corresponds to the $t$ test statistic (t = 2.26).

Assuming that the null hypothesis is true ($\mu = 3.6$ grams) how likely is it to observe a sample as extreme as or more extreme than almonds_sample_100? Or correspondingly, how likely is it to observe a sample mean as extreme as or more extreme than $\overline x = 0.36$? Or even, how likely is it to observe a test statistic that is $t = 2.26$ units or more away from the center of the $t$ distribution?

Because this is a two-sided test, we care about extreme values that are 2.26 away in either direction of the distribution. The shaded regions on both tails of the $t$ distribution in Figure 9.1 represent the probability of these extreme values.

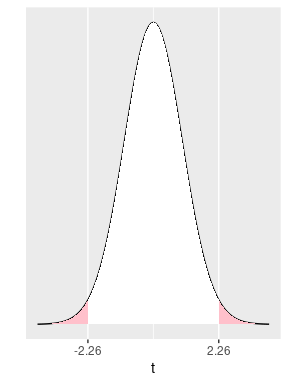
FIGURE 9.1: The tails of a t curve for this hypothesis test.

The function pt() finds the area under a $t$ curve to the left of a given value. The function requires the argument q (quantile) that in our example is the value of $t$ on the left part of the plot (-2.26) and the argument df, the degrees of freedom that for a one-sample test are $n-1$. The sample size of almonds_sample_100 was $n = 100$. Finally, since we need the area on both tails and the $t$ distribution is symmetric, we simply multiply the results by 2:

2 * pt(q = -2.26, df = 100 - 1)

We have determined that, assuming that the null hypothesis is true, the probability of getting a sample as extreme as or more extreme than almonds_sample_100 is 0.026. This probability is called the $p$-value.

What does this mean? Well, most statistics textbooks will state that, given a significance level, often set as $\alpha = 0.05$, if the $p$-value is less than $\alpha$, we reject the null hypothesis. While technically not incorrect, this type of statement does not provide enough insight for students to fully understand the conclusion.

Let’s unpack some of these elements and provide additional context to them:

The key element of the conclusion is to determine whether the statement under the null hypothesis can be rejected. If assuming that the null hypothesis is true, it is very unlikely (almost impossible) to observe a random sample such as the one we have observed, we need to reject the null hypothesis, but we would not reject the null hypothesis in any other situation. In that sense, the null hypothesis has a privileged status. The reason for this is that we do not want to make a mistake and reject the null hypothesis when the claim under it is actually true. In statistics, making this mistake is called a Type I Error. So, we only reject the null hypothesis if the chances of committing a Type I Error are truly small. The significance level, denoted by the Greek letter $\alpha$ (pronounced “alpha”), is precisely the probability of committing a Type I Error.

What are the chances you are willing to take? Again, $\alpha = 0.05$ is what most textbooks use and many research communities have adopted for decades. While we should be able to work with this number, after all we may need to interact with people that are used to it, we want to treat it as one of many possible numbers.

The significance level, $\alpha$, is a predefined level of accepted uncertainty. This value should be defined well before the $p$-value has been calculated, or even before data has been collected. Ideally, it should represent our tolerance for uncertainty. But, how can we determine what this value should be?

We provide an example. Assume that you are a student and have to take a test in your statistics class worth 100 points. You have studied for it, and you expect to get a passing grade (score in the 80s) but not better than that. The day of the exam the instructor gives you one additional option. You can take the exam and receive a grade based on your performance or you can play the following game: the instructor rolls a six-sided fair die. If the top face shows a “one” you score zero on your test, otherwise you score 100. There is a 1 in 6 chance that you get zero. Would you play this game?

If you would not play the game, let’s change it. Now the instructor rolls the die twice, you score 0 in the test only if both rolls are “one.” Otherwise, you score 100. There is only a 1 in 36 chance to get zero. Would you now play this game?

What if the instructor rolls the die five times and you score zero in the test only if each roll is a “one,” and you score 100 otherwise. The is only a 1 in 7776 chance to get zero. Would you play this game?

Converted to probabilities, the three games shown above give you the probabilities of getting a zero equal to $1/6 = 0.167$, $1/36 = 0.028$, and $1/7776 = 0.0001$, respectively. Think of these as $p$-values and getting a zero in the test as committing a Type I Error.

In the context of a hypothesis test, when the random sample collected is extreme, the $p$-value is really small, and we reject the null hypothesis, there is always a chance that the null hypothesis was true, the random sample collected was very atypical, and these results led us to commit a Type I Error. There is always uncertainty when using random samples to make inferences about populations. All we can do is decide what is our level of tolerance for this uncertainty. Is it $1/6 = 0.167$, $1/36 = 0.028$, $1/7776 = 0.0001$, or some other level? This is precisely the significance level $\alpha$.

Returning to the almond example, if we had set $\alpha = 0.04$ and we observed the $p$-value = 0.026, we would reject the null hypothesis and conclude that the population mean $\mu$ is not equal to 3.6 grams. When the null hypothesis is rejected we say that the result of the test is statistically significant.

Let’s summarize the steps for hypothesis testing:

Based on the claim we are planning to test, state the null and alternative hypothesis in terms of $\mu$.
- Remember that the equal sign should go under the null hypothesis as this is needed for the method.
- The statement under the null hypothesis is assumed to be true during the process.
- Typically, researchers want to conclude in favor of the alternative hypothesis; that is, they try to see if the data provides evidence against the null hypothesis.
Set a significance level $\alpha$, based on your tolerance for committing a Type I Error, always before working with the sample.
Obtain the sample mean, sample standard deviation, $t$-test statistic, and $p$-value.
- When working with a two-sided test, as in the almond example above, the $p$-value is the area on both tails.
- For a left-sided test, find the area under the $t$ distribution to the left of the observed $t$ test statistic.
- For a right-sided test, find the area under the $t$ distribution to the right of the observed $t$ test statistic.
Determine whether the result of the test is statistically significant (if the null is rejected) or non-significant (the null is not rejected).

The simulation-based approach

When using a simulation-based approach such as the bootstrap percentile method, we repeat the first two steps of the theory-based approach:

State the null and alternative hypothesis in terms of $\mu$. The statement under the null hypothesis is assumed to be true during the process.
Set a significance level, $\alpha$, based on your tolerance for committing a Type I Error.

In step 1 we need to assume the null hypothesis is true. This presents a technical complication in the bootstrap percentile method as the sample collected and corresponding bootstrap samples are based on the real distribution and if the null hypothesis is not true they cannot reflect this. The solution is to shift the sample values by a constant so as to make the sample mean equal to the claimed population mean under the null hypothesis.

The infer workflow takes this into account automatically, but when introduced to students for the first time, the additional shifting tends to create some confusion in the intuition of the method. We have determined that it is easier to introduce the elements of the simulation-based approach to hypothesis testing via the two-sample problem context using another resampling technique called permutation. Details of this method are presented in Sections 9.3, 9.4, and 9.5. Once we are very comfortable using this method, we can then explore the bootstrap percentile method for one-sample problems. Observe that more examples with explanations for the simulation-based approach are presented in the Appendices online including an example of a one-sample mean hypothesis test using simulation-based methods.

For completeness, we present here the code and results of the one-sample hypothesis test for the almonds’ problem.

null_dist <- almonds_sample_100 |>
  specify(response = weight) |>
  hypothesize(null = "point", mu = 3.6) |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate(stat = "mean")

x_bar_almonds <- almonds_sample_100 |>
  summarize(sample_mean = mean(weight)) |>
  select(sample_mean)
null_dist |>
  get_p_value(obs_stat = x_bar_almonds, direction = "two-sided")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.032

The $p$-value is 0.032. This is fairly similar to the $p$-value obtained using the theory-based approach. Using the same significance level $\alpha = 0.04$ we again reject the null hypothesis.

9.1.2 Hypothesis tests and confidence intervals

Even though hypothesis tests and confidence intervals are two different approaches that have different goals, they complement each other. For example, in Subsection 8.1.4 we calculated the 95% confidence interval for the almonds’ mean weight, $\mu$, using the sample almonds_sample_100. The theory-based approach was given by

\[ \begin{aligned} \left(\overline{x} - 1.98 \frac{s}{\sqrt{n}},\quad \overline{x} + 1.98 \frac{s}{\sqrt{n}}\right) \end{aligned} \]

and the 95% confidence interval is:

almonds_sample_100 |>
  summarize(lower_bound = mean(weight) - 1.98*sd(weight)/sqrt(length(weight)),
            upper_bound = mean(weight) + 1.98*sd(weight)/sqrt(length(weight)))

# A tibble: 1 × 2
  lower_bound upper_bound
        <dbl>       <dbl>
1     3.61028     3.75372

Using the simulation-based approach via the bootstrap percentile method, the 95% confidence interval is

bootstrap_means <- almonds_sample_100 |> 
  specify(response = weight) |> 
  generate(reps = 1000, type = "bootstrap") |> 
  calculate(stat = "mean")

bootstrap_means |> 
  get_confidence_interval(level = 0.95, type = "percentile")

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1  3.61198    3.756

Both 95% confidence intervals are very similar and, more importantly, both intervals do not contain $\mu = 3.6$ grams. Recall that when performing hypothesis testing we rejected the null hypothesis, $H_0: \mu = 3.6$. The results obtained using confidence intervals are consistent to the conclusions of hypothesis testing.

In general, if the values for $\mu$ under the null hypothesis are not part of the confidence interval, the null hypothesis is rejected. Note, however, that the confidence level used when constructing the interval, 95% in our example, needs to be consistent with the significance level, $\alpha$, used for the hypothesis test. In particular, when the hypothesis test is two-sided and a significance level $\alpha$ is used, we calculate a confidence interval for a confidence level equal to $(1 - \alpha)\times 100\%$. For example, if $\alpha = 0.05$ then the corresponding confidence level is $(1 - 0.05) = 0.95$ or $95\%$. The correspondence is direct because the confidence intervals that we calculate are always two-sided. On the other hand, if the hypothesis test used is one-sided (left or right), calculate a confidence interval with a confidence level equal to $(1 - 2\alpha)\times 100\%$. For example, if $\alpha = 0.05$ then, the corresponding confidence level needed is $(1 - 2\cdot 0.05) = 0.9$ or $90\%$.

This section concludes our discussion about one-sample hypothesis tests. Observe that, as we have done for confidence intervals, we can also construct hypothesis tests for proportions, and when using the bootstrap percentile method, we can do it also for other quantities, such as the population median, quartiles, etc.

We focus now on building hypothesis tests for two-sample problems.

9.2 Music popularity activity

Let’s start with an activity studying the effect of music genre on Spotify song popularity.

9.2.1 Is metal music more popular than deep house music?

Imagine you are a music analyst for Spotify, and you are curious about whether fans of metal or deep house are more passionate about their favorite genres. You want to determine if there’s a significant difference in the popularity of these two genres. Popularity, in this case, is measured by Spotify, say, as the average number of streams and recent user interactions on tracks classified under each genre. (Note that Spotify does not actually disclose how this metric is calculated, so we have to take our best guess.) This question sets the stage for our exploration into hypothesis testing.

Metal music, characterized by its aggressive sounds, powerful vocals, and complex instrumentals, has cultivated a loyal fanbase that often prides itself on its deep appreciation for the genre’s intensity and technical skill. On the other hand, deep house music, with its smooth, soulful rhythms and steady beats, attracts listeners who enjoy the genre’s calming and immersive vibe, often associated with late-night clubs and chill-out sessions.

By comparing the popularity metrics between these two genres, we can determine if one truly resonates more with listeners on Spotify. This exploration not only deepens our understanding of musical preferences but also serves as a practical introduction to the principles of hypothesis testing.

To begin the analysis, 2000 tracks were selected at random from Spotify’s song archive. We will use “song” and “track” interchangeably going forward. There were 1000 metal tracks and 1000 deep house tracks selected.

The moderndive package contains the data on the songs by genre in the spotify_by_genre data frame. There are six genres selected in that data (country, deep-house, dubstep, hip-hop, metal, and rock). You will have the opportunity to explore relationships with the other genres and popularity in the Learning checks. Let’s explore this data by focusing on just metal and deep-house by looking at 12 randomly selected rows and our columns of interest in Table 9.2. Note that we also group our selection so that each of the four possible groupings of track_genre and popular_or_not are selected.

spotify_metal_deephouse <- spotify_by_genre |> 
  filter(track_genre %in% c("metal", "deep-house")) |> 
  select(track_genre, artists, track_name, popularity, popular_or_not) 
spotify_metal_deephouse |>
  group_by(track_genre, popular_or_not) |> 
  sample_n(size = 3)

TABLE 9.2: Sample of twelve songs from the Spotify data frame.
track_genre	artists	track_name	popularity	popular_or_not
deep-house	LYOD;Tom Auton	On My Way	51	popular
deep-house	Sunmoon	Just the Two of Us	52	popular
deep-house	Tensnake;Nazzereene	Latching Onto You	51	popular
metal	Slipknot	Psychosocial	66	popular
deep-house	BCX	Miracle In The Middle Of My Heart - Original Mix	41	not popular
metal	blessthefall	I Wouldn’t Quit If Everyone Quit	0	not popular
deep-house	Junge Junge;Tyron Hapi	I’m The One - Tyron Hapi Remix	49	not popular
metal	Poison	Every Rose Has Its Thorn - Remastered 2003	0	not popular
metal	Armored Dawn	S.O.S.	54	popular
deep-house	James Hype;Pia Mia;PS1	Good Luck (feat. Pia Mia) - PS1 Remix	47	not popular
metal	Hollywood Undead	Riot	26	not popular
metal	Breaking Benjamin	Ashes of Eden	61	popular

The track_genre variable indicates what genre the song is classified under, the artists and track_name columns provide additional information about the track by providing the artist and the name of the song, popularity is the metric mentioned earlier given by Spotify, and popular_or_not is a categorical representation of the popularity column with any value of 50 (the 75th percentile of popularity) referring to popular and anything at or below 50 as not_popular. The decision made by the authors to call a song “popular” if it is above the 75th percentile (3rd quartile) of popularity is arbitrary and could be changed to any other value.)

Let’s perform an exploratory data analysis of the relationship between the two categorical variables track_genre and popular_or_not. Recall that we saw in Subsection 2.8.3 that one way we can visualize such a relationship is by using a stacked barplot.

ggplot(spotify_metal_deephouse, aes(x = track_genre, fill = popular_or_not)) +
  geom_bar() +
  labs(x = "Genre of track")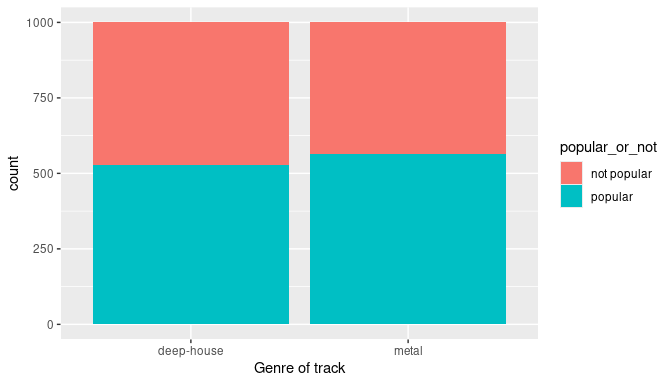

FIGURE 9.2: Barplot relating genre to popularity.

Observe in Figure 9.2 that, in this sample, metal songs are only slightly more popular than deep house songs by looking at the height of the popular bars. Let’s quantify these popularity rates by computing the proportion of songs classified as popular for each of the two genres using the dplyr package for data wrangling. Note the use of the tally() function here which is a shortcut for summarize(n = n()) to get counts.

spotify_metal_deephouse |> 
  group_by(track_genre, popular_or_not) |>
  tally() # Same as summarize(n = n())

# A tibble: 4 × 3
# Groups:   track_genre [2]
  track_genre popular_or_not     n
  <chr>       <chr>          <int>
1 deep-house  not popular      471
2 deep-house  popular          529
3 metal       not popular      437
4 metal       popular          563

So of the 1000 metal songs, 563 were popular, for a proportion of 563/1000 = 0.563 = 56.3%. On the other hand, of the 1000 deep house songs, 529 were popular, for a proportion of 529/1000 = 0.529 = 52.9%. Comparing these two rates of popularity, it appears that metal songs were popular at a rate 0.563 $-$ 0.529 = 0.034 = 3.4% higher than deep house songs. This is suggestive of an advantage for metal songs in terms of popularity.

The question is, however, does this provide conclusive evidence that there is greater popularity for metal songs compared to deep house songs? Could a difference in popularity rates of 3.4% still occur by chance, even in a hypothetical world where no difference in popularity existed between the two genres? In other words, what is the role of sampling variation in this hypothesized world? To answer this question, we will again rely on a computer to run simulations.

9.2.2 Shuffling once

First, try to imagine a hypothetical universe where there was no difference in the popularity of metal and deep house. In such a hypothetical universe, the genre of a song would have no bearing on their chances of popularity. Bringing things back to our spotify_metal_deephouse data frame, the popular_or_not variable would thus be an irrelevant label. If these popular_or_not labels were irrelevant, then we could randomly reassign them by “shuffling” them to no consequence!

To illustrate this idea, let’s narrow our focus to 52 chosen songs of the 2000 that you saw earlier. The track_genre column shows what the original genre of the song was. Note that to keep this smaller dataset of 52 rows to be a representative sample of the 2000 rows, we have sampled such that the popularity rate for each of metal and deep-house is close to the original rates of 0.563 and 0.529, respectively, prior to shuffling. This data is available in the spotify_52_original data frame in the moderndive package. We also remove the track_id column for simplicity. It is an identification variable that is not relevant for our analysis. A sample of this is shown in Table 9.3.

spotify_52_original |> 
  select(-track_id) |> 
  head(10)

TABLE 9.3: Representative sample of metal and deep-house songs
track_genre	artists	track_name	popularity	popular_or_not
deep-house	Jess Bays;Poppy Baskcomb	Temptation (feat. Poppy Baskcomb)	63	popular
metal	Whitesnake	Here I Go Again - 2018 Remaster	69	popular
metal	Blind Melon	No Rain	1	not popular
metal	Avenged Sevenfold	Shepherd of Fire	70	popular
deep-house	Nora Van Elken	I Wanna Dance With Somebody (Who Loves Me) - Summer Edit	56	popular
metal	Breaking Benjamin	Ashes of Eden	61	popular
metal	Bon Jovi	Thank You For Loving Me	67	popular
deep-house	Starley;Bad Paris	Arms Around Me - Bad Paris Remix	55	popular
deep-house	The Him;LissA	I Wonder	43	not popular
metal	Deftones	Ohms	0	not popular

In our hypothesized universe of no difference in genre popularity, popularity is irrelevant and thus it is of no consequence to randomly “shuffle” the values of popular_or_not. The popular_or_not column in the spotify_52_shuffled data frame in the moderndive package shows one such possible random shuffling.

spotify_52_shuffled |> 
  select(-track_id) |> 
  head(10)

TABLE 9.4: Shuffled version of `popular_or_not` in sample
track_genre	artists	track_name	popularity	popular_or_not
deep-house	Jess Bays;Poppy Baskcomb	Temptation (feat. Poppy Baskcomb)	63	popular
metal	Whitesnake	Here I Go Again - 2018 Remaster	69	not popular
metal	Blind Melon	No Rain	1	popular
metal	Avenged Sevenfold	Shepherd of Fire	70	not popular
deep-house	Nora Van Elken	I Wanna Dance With Somebody (Who Loves Me) - Summer Edit	56	popular
metal	Breaking Benjamin	Ashes of Eden	61	not popular
metal	Bon Jovi	Thank You For Loving Me	67	not popular
deep-house	Starley;Bad Paris	Arms Around Me - Bad Paris Remix	55	not popular
deep-house	The Him;LissA	I Wonder	43	not popular
metal	Deftones	Ohms	0	not popular

Observe in Table 9.4 that the popular_or_not column how the popular and not popular results are now listed in a different order. Some of the original popular now are not popular, some of the not popular are popular, and others are the same as the original.

Again, such random shuffling of the popular_or_not label only makes sense in our hypothesized universe of no difference in popularity between genres. Is there a tactile way for us to understand what is going on with this shuffling? One way would be by using a standard deck of 52 playing cards, which we display in Figure 9.3.

FIGURE 9.3: Standard deck of 52 playing cards.

Since we started with equal sample sizes of 1000 songs for each genre, we can think about splitting the deck in half to have 26 cards in two piles (one for metal and another for deep-house). After shuffling these 52 cards as seen in Figure 9.4, we split the deck equally into the two piles of 26 cards each. Then, we can flip the cards over one-by-one, assigning “popular” for each red card and “not popular” for each black card keeping a tally of how many of each genre are popular.

FIGURE 9.4: Shuffling a deck of cards.

Let’s repeat the same exploratory data analysis we did for the original spotify_metal_deephouse data on our spotify_52_original and spotify_52_shuffled data frames. Let’s create a barplot visualizing the relationship between track_genre and the new shuffled popular_or_not variable, and compare this to the original un-shuffled version in Figure 9.5.

ggplot(spotify_52_shuffled, aes(x = track_genre, fill = popular_or_not)) +
  geom_bar() + 
  labs(x = "Genre of track")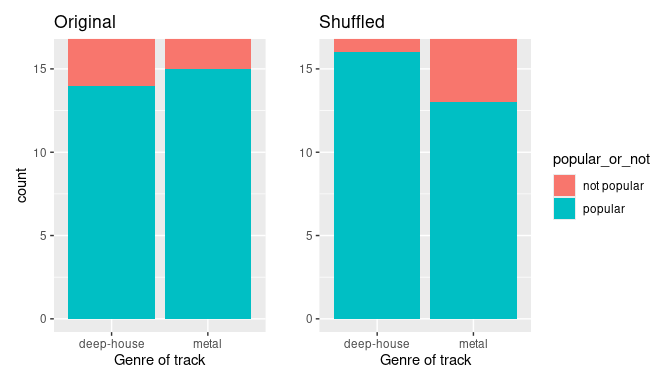

FIGURE 9.5: Barplots of relationship of genre with popular or not' (left) and shuffledpopular or not’ (right).

The difference in metal versus deep house popularity rates is now different. Compared to the original data in the left barplot, the new “shuffled” data in the right barplot has popularity rates that are actually in the opposite direction as they were originally. This is because the shuffling process has removed any relationship between genre and popularity.

Let’s also compute the proportion of tracks that are now “popular” in the popular_or_not column for each genre:

spotify_52_shuffled |> 
  group_by(track_genre, popular_or_not) |> 
  tally()

# A tibble: 4 × 3
# Groups:   track_genre [2]
  track_genre popular_or_not     n
  <chr>       <chr>          <int>
1 deep-house  not popular       10
2 deep-house  popular           16
3 metal       not popular       13
4 metal       popular           13

So in this one sample of a hypothetical universe of no difference in genre popularity, $13/26 = 0.5 = 50\%$ of metal songs were popular. On the other hand, $16/26 = 0.615 = 61.5\%$ of deep house songs were popular. Let’s next compare these two values. It appears that metal tracks were popular at a rate that was $0.5 - 0.615 = -0.115 = -11.5\%$ different than deep house songs.

Observe how this difference in rates is not the same as the difference in rates of 0.034 = 3.4% we originally observed. This is once again due to sampling variation. How can we better understand the effect of this sampling variation? By repeating this shuffling several times!

9.2.3 What did we just do?

What we just demonstrated in this activity is the statistical procedure known as hypothesis testing using a permutation test. The term “permutation” is the mathematical term for “shuffling”: taking a series of values and reordering them randomly, as you did with the playing cards. In fact, permutations are another form of resampling, like the bootstrap method you performed in Chapter 8. While the bootstrap method involves resampling with replacement, permutation methods involve resampling without replacement.

We do not need restrict our analysis to a dataset of 52 rows only. It is useful to manually shuffle the deck of cards and assign values of popular or not popular to different songs, but the same ideas can be applied to each of the 2000 tracks in our spotify_metal_deephouse data. We can think with this data about an inference about an unknown difference in population proportions with the 2000 tracks being our sample. We denote this as $p_{m} - p_{d}$, where $p_{m}$ is the population proportion of songs with metal names being popular and $p_{d}$ is the equivalent for deep house songs. Recall that this is one of the scenarios for inference we have seen so far in Table 9.5.

TABLE 9.5: Scenarios of sampling for inference
Scenario	Population parameter	Notation	Point estimate	Symbol(s)
1	Population proportion	$p$	Sample proportion	$\widehat{p}$
2	Population mean	$\mu$	Sample mean	$\overline{x}$ or $\widehat{\mu}$
3	Difference in population proportions	$p_1 - p_2$	Difference in sample proportions	$\widehat{p}_1 - \widehat{p}_2$

So, based on our sample of $n_m = 1000$ metal tracks and $n_f = 1000$ deep house tracks, the point estimate for $p_{m} - p_{d}$ is the difference in sample proportions

\[\widehat{p}_{m} -\widehat{p}_{f} = 0.563 - 0.529 = 0.034 = 3.4\%\].

This difference in favor of metal songs of 0.034 is greater than 0, suggesting metal songs are more popular than deep house songs.

However, the question we ask ourselves was “is this difference meaningfully greater than 0?”. In other words, is that difference indicative of true popularity, or can we just attribute it to sampling variation? Hypothesis testing allows us to make such distinctions.

9.3 Understanding hypothesis tests

Much like the terminology, notation, and definitions relating to sampling you saw in Section 7.2, there are a lot of terminology, notation, and definitions related to hypothesis testing as well. Some of this was introduced in Section 9.1. Learning these may seem like a very daunting task at first. However, with practice, practice, and more practice, anyone can master them.

First, a hypothesis is a statement about the value of an unknown population parameter. In our genre popularity activity, our population parameter of interest is the difference in population proportions $p_{m} - p_{d}$. Hypothesis tests can involve any of the population parameters in Table 8.1 of the five inference scenarios we will cover in this book and also more advanced types we will not cover here.

Second, a hypothesis test consists of a test between two competing hypotheses: (1) a null hypothesis $H_0$ (pronounced “H-naught”) versus (2) an alternative hypothesis $H_A$ (also denoted $H_1$).

When working with the comparison of two populations parameters, typically, the null hypothesis is a claim that there is “no effect” or “no difference of interest.” In many cases, the null hypothesis represents the status quo. Furthermore, the alternative hypothesis is the claim the experimenter or researcher wants to establish or find evidence to support. It is viewed as a “challenger” hypothesis to the null hypothesis $H_0$. In our genre popularity activity, an appropriate hypothesis test would be:

\[ \begin{aligned} H_0 &: \text{metal and deep house have the same popularity rate}\\ \text{vs } H_A &: \text{metal is popular at a higher rate than deep house} \end{aligned} \]

Note some of the choices we have made. First, we set the null hypothesis $H_0$ to be that there is no difference in popularity rate and the “challenger” alternative hypothesis $H_A$ to be that there is a difference in favor of metal. As discussed earlier, the null hypothesis is set to reflect a situation of “no change.” As we discussed earlier, in this case, $H_0$ corresponds to there being no difference in popularity. Furthermore, we set $H_A$ to be that metal is popular at a higher rate, a subjective choice reflecting a prior suspicion we have that this is the case. As discussed earlier this is a one-sided test. It can be left- or right-sided, and this becomes clear once we express it in terms of proportions. If someone else however does not share such suspicions and only wants to investigate that there is a difference, whether higher or lower, they would construct a two-sided test.

We can re-express the formulation of our hypothesis test using the mathematical notation for our population parameter of interest, the difference in population proportions $p_{m} - p_{d}$:

\[ \begin{aligned} H_0 &: p_{m} - p_{d} = 0\\ \text{vs } H_A&: p_{m} - p_{d} > 0 \end{aligned} \]

Observe how the alternative hypothesis $H_A$ is written $p_{m} - p_{d} > 0$. Since we have chosen this particular formulation, the one-sided test becomes right-sided because we are looking for a difference that is greater than zero as evidence to reject the null hypothesis. Had we opted for a two-sided alternative, we would have set $p_{m} - p_{d} \neq 0$. We work here with the right-sided test and will present an example of a two-sided test in Section 9.6.

Third, a test statistic is a point estimate/sample statistic formula used for hypothesis testing. Note that a sample statistic is merely a summary statistic based on a sample of observations. Recall we saw in Section 3.3 that a summary statistic takes in many values and returns only one. Here, the samples would be the $n_m = 1000$ metal songs and the $n_f = 1000$ deep house songs. Hence, the point estimate of interest is the difference in sample proportions $\widehat{p}_{m} - \widehat{p}_{d}$.

Fourth, the observed test statistic is the value of the test statistic that we observed in real life. In our case, we computed this value using the data saved in the spotify_metal_deephouse data frame. It was the observed difference of $\widehat{p}_{m} -\widehat{p}_{d} = 0.563 - 0.529 = 0.034 = 3.4\%$ in favor of metal songs.

Fifth, the null distribution is the sampling distribution of the test statistic assuming the null hypothesis $H_0$ is true. Let’s unpack these ideas slowly. The key to understanding the null distribution is that the null hypothesis $H_0$ is assumed to be true. We are not saying that $H_0$ is true at this point, we are only assuming it to be true for hypothesis-testing purposes. In our case, this corresponds to our hypothesized universe of no difference in popularity rates. Assuming the null hypothesis $H_0$, also stated as “Under $H_0$,” how does the test statistic vary due to sampling variation? In our case, how will the difference in sample proportions $\widehat{p}_{m} - \widehat{p}_{f}$ vary due to sampling under $H_0$? Recall from Subsection 7.3.4 that distributions displaying how point estimates vary due to sampling variation are called sampling distributions. The only additional thing to keep in mind about null distributions is that they are sampling distributions assuming the null hypothesis $H_0$ is true.

Sixth, the $p$-value is the probability of obtaining a test statistic just as extreme as or more extreme than the observed test statistic assuming the null hypothesis $H_0$ is true. You can think of the $p$-value as a quantification of “surprise”: assuming $H_0$ is true, how surprised are we with what we observed? Or in our case, in our hypothesized universe of no difference in genre popularity, how surprised are we that we observed higher popularity rates of 0.034 from our collected samples if no difference in genre popularity exists? Very surprised? Somewhat surprised?

The $p$-value quantifies this probability, or what proportion had a more “extreme” result? Here, extreme is defined in terms of the alternative hypothesis $H_A$ that metal popularity is at a higher rate than deep house. In other words, how often was the popularity of metal even more pronounced than $0.563 - 0.529 = 0.034 = 3.4\%$?

Seventh and lastly, in many hypothesis testing procedures, it is commonly recommended to set the significance level of the test beforehand. It is denoted by $\alpha$. Please review our discussion of $\alpha$ in Section 9.1.1 when we discussed the theory-based approach. For now, it is sufficient to recall that if the $p$-value is less than or equal to $\alpha$, we reject the null hypothesis $H_0$.

Alternatively, if the $p$-value is greater than $\alpha$, we would “fail to reject $H_0$.” Note the latter statement is not quite the same as saying we “accept $H_0$.” This distinction is rather subtle and not immediately obvious. So we will revisit it later in Section 9.5.

While different fields tend to use different values of $\alpha$, some commonly used values for $\alpha$ are 0.1, 0.01, and 0.05; with 0.05 being the choice people often make without putting much thought into it. We will talk more about $\alpha$ significance levels in Section 9.5, but first let’s fully conduct a hypothesis test corresponding to our genre popularity activity using the infer package.

9.4 Conducting hypothesis tests

In Section 8.2.2, we showed you how to construct confidence intervals. We first illustrated how to do this using dplyr data wrangling verbs and the rep_sample_n() function from Subsection 7.1.3 which we used as a virtual shovel. In particular, we constructed confidence intervals by resampling with replacement by setting the replace = TRUE argument to the rep_sample_n() function.

We then showed you how to perform the same task using the infer package workflow. While both workflows resulted in the same bootstrap distribution from which we can construct confidence intervals, the infer package workflow emphasizes each of the steps in the overall process in Figure 9.6. It does so using function names that are intuitively named with verbs:

specify() the variables of interest in your data frame.
generate() replicates of bootstrap resamples with replacement.
calculate() the summary statistic of interest.
visualize() the resulting bootstrap distribution and confidence interval.

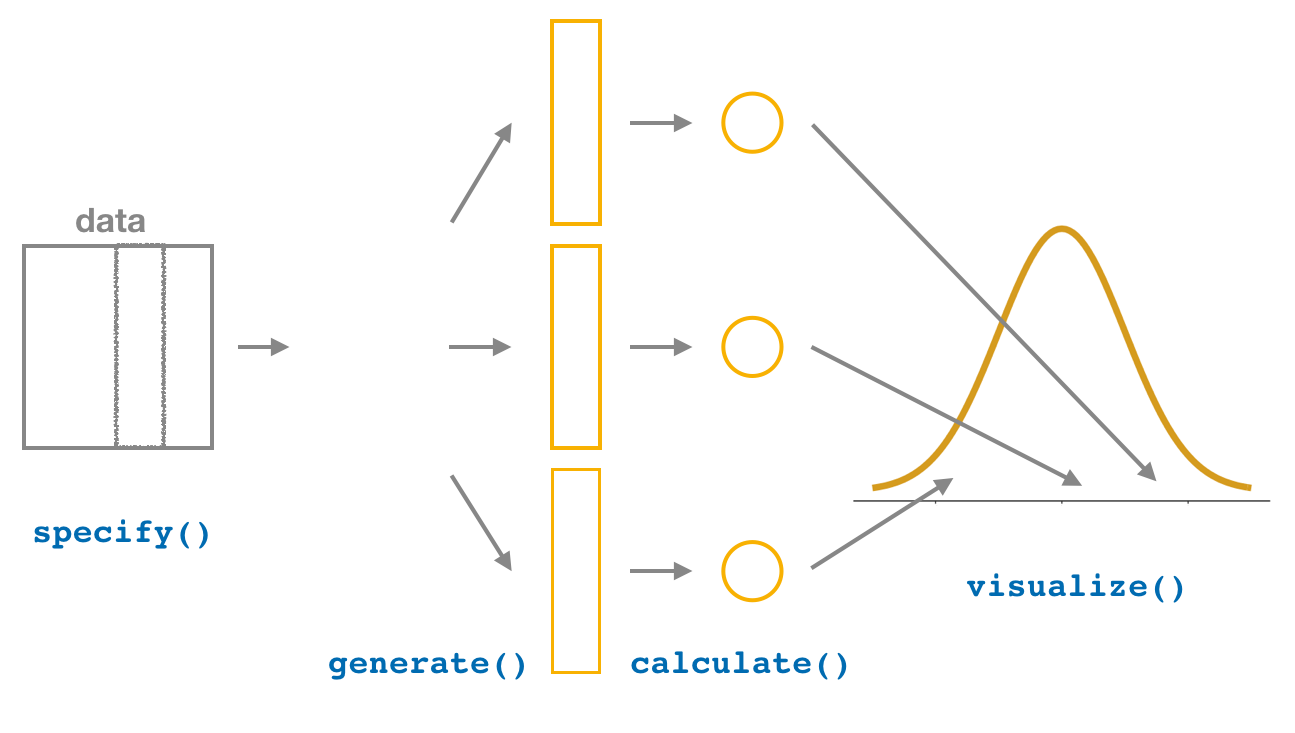
FIGURE 9.6: Confidence intervals with the infer package.

In this section, we will now show you how to seamlessly modify the previously seen infer code for constructing confidence intervals to conduct hypothesis tests. You will notice that the basic outline of the workflow is almost identical, except for an additional hypothesize() step between the specify() and generate() steps, as can be seen in Figure 9.7.

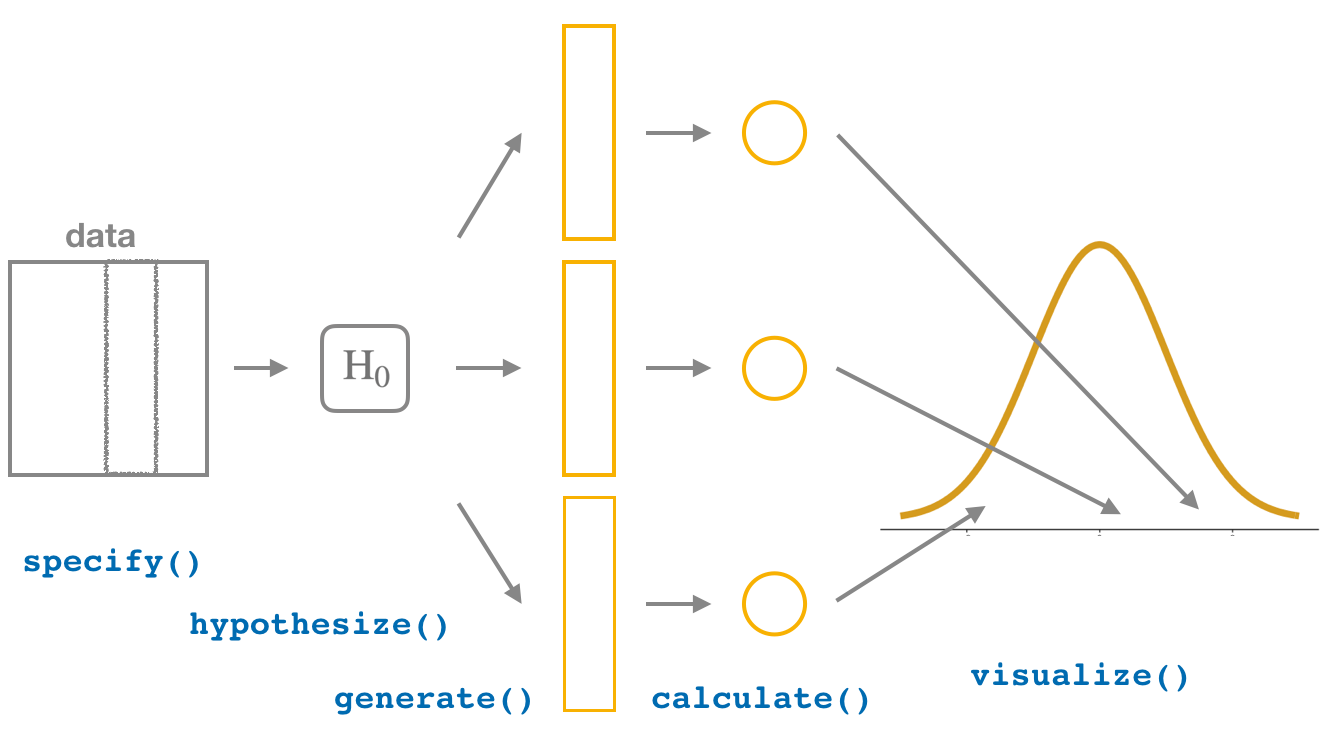
FIGURE 9.7: Hypothesis testing with the infer package.

Furthermore, we will use a pre-specified significance level $\alpha$ = 0.1 for this hypothesis test. Please read the discussion about $\alpha$ in Subsection 9.1.1 or later on in Section 9.5.

9.4.1 `infer` package workflow

1. `specify` variables

Recall that we use the specify() verb to specify the response variable and, if needed, any explanatory variables for our study. In this case, since we are interested in any potential effects of genre on popularity rates, we set popular_or_not as the response variable and track_genre as the explanatory variable. We do so using formula = response ~ explanatory where response is the name of the response variable in the data frame and explanatory is the name of the explanatory variable. So in our case it is popular_or_not ~ track_genre.

Furthermore, since we are interested in the proportion of songs "popular", and not the proportion of songs not popular, we set the argument success to "popular".

spotify_metal_deephouse |> 
  specify(formula = popular_or_not ~ track_genre, success = "popular")

Response: popular_or_not (factor)
Explanatory: track_genre (factor)
# A tibble: 2,000 × 2
   popular_or_not track_genre
   <fct>          <fct>      
 1 popular        deep-house 
 2 popular        deep-house 
 3 popular        deep-house 
 4 popular        deep-house 
 5 popular        deep-house 
 6 popular        deep-house 
 7 popular        deep-house 
 8 popular        deep-house 
 9 popular        deep-house 
10 popular        deep-house 
# ℹ 1,990 more rows

Again, notice how the spotify_metal_deephouse data itself does not change, but the Response: popular_or_not (factor) and Explanatory: track_genre (factor) meta-data do. This is similar to how the group_by() verb from dplyr does not change the data, but only adds “grouping” meta-data, as we saw in Section 3.4. We also now focus on only the two columns of interest in the data for our problem at hand with popular_or_not and track_genre.

2. `hypothesize` the null

In order to conduct hypothesis tests using the infer workflow, we need a new step not present for confidence intervals: hypothesize(). Recall from Section 9.3 that our hypothesis test was

\[ \begin{aligned} H_0 &: p_{m} - p_{d} = 0\\ \text{vs. } H_A&: p_{m} - p_{d} > 0 \end{aligned} \]

In other words, the null hypothesis $H_0$ corresponding to our “hypothesized universe” stated that there was no difference in genre popularity rates. We set this null hypothesis $H_0$ in our infer workflow using the null argument of the hypothesize() function to either:

"point" for hypotheses involving a single sample or
"independence" for hypotheses involving two samples.

In our case, since we have two samples (the metal songs and the deep house songs), we set null = "independence".

spotify_metal_deephouse |> 
  specify(formula = popular_or_not ~ track_genre, success = "popular") |> 
  hypothesize(null = "independence")

Response: popular_or_not (factor)
Explanatory: track_genre (factor)
Null Hypothesis: independence
# A tibble: 2,000 × 2
   popular_or_not track_genre
   <fct>          <fct>      
 1 popular        deep-house 
 2 popular        deep-house 
 3 popular        deep-house 
 4 popular        deep-house 
 5 popular        deep-house 
 6 popular        deep-house 
 7 popular        deep-house 
 8 popular        deep-house 
 9 popular        deep-house 
10 popular        deep-house 
# ℹ 1,990 more rows

Again, the data has not changed yet. This will occur at the upcoming generate() step; we are merely setting meta-data for now.

Where do the terms "point" and "independence" come from? These are two technical statistical terms. The term “point” relates from the fact that for a single group of observations, you will test the value of a single point. Going back to the pennies example from Chapter 8, say we wanted to test if the mean weight of all chocolate-covered almonds was equal to 3.5 grams or not. We would be testing the value of a “point” $\mu$, the mean weight in grams of all chocolate-covered almonds, as follows

\[ \begin{aligned} H_0 &: \mu = 3.5\\ \text{vs } H_A&: \mu \neq 3.5 \end{aligned} \]

The term “independence” relates to the fact that for two groups of observations, you are testing whether or not the response variable is independent of the explanatory variable that assigns the groups. In our case, we are testing whether the popular_or_not response variable is “independent” of the explanatory variable track_genre.

3. `generate` replicates

After we hypothesize() the null hypothesis, we generate() replicates of “shuffled” datasets assuming the null hypothesis is true. We do this by repeating the shuffling exercise you performed in Section 9.2 several times on the full dataset of 2000 rows. Let’s use the computer to repeat this 1000 times by setting reps = 1000 in the generate() function. However, unlike for confidence intervals where we generated replicates using type = "bootstrap" resampling with replacement, we will now perform shuffles/permutations by setting type = "permute". Recall that shuffles/permutations are a kind of resampling, but unlike the bootstrap method, they involve resampling without replacement.

spotify_generate <- spotify_metal_deephouse |> 
  specify(formula = popular_or_not ~ track_genre, success = "popular") |> 
  hypothesize(null = "independence") |> 
  generate(reps = 1000, type = "permute")
nrow(spotify_generate)

[1] 2000000

The resulting data frame has 2,000,000 rows. This is because we performed shuffles/permutations for each of the 2000 rows 1000 times and $2,000,000 = 1000 \cdot 2000$. If you explore the spotify_generate data frame with View(), you will notice that the variable replicate indicates which resample each row belongs to. So it has the value 1 2000 times, the value 2 2000 times, all the way through to the value 1000 2000 times.

4. `calculate` summary statistics

Now that we have generated 1000 replicates of “shuffles” assuming the null hypothesis is true, let’s calculate() the appropriate summary statistic for each of our 1000 shuffles. From Section 9.3, point estimates related to hypothesis testing have a specific name: test statistics. Since the unknown population parameter of interest is the difference in population proportions $p_{m} - p_{d}$, the test statistic here is the difference in sample proportions $\widehat{p}_{m} - \widehat{p}_{f}$.

For each of our 1000 shuffles, we can calculate this test statistic by setting stat = "diff in props". Furthermore, since we are interested in $\widehat{p}_{m} - \widehat{p}_{d}$ we set order = c("metal", "deep-house"). As we stated earlier, the order of the subtraction does not matter, so long as you stay consistent throughout your analysis and tailor your interpretations accordingly. Let’s save the result in a data frame called null_distribution:

null_distribution <- spotify_metal_deephouse |> 
  specify(formula = popular_or_not ~ track_genre, success = "popular") |> 
  hypothesize(null = "independence") |> 
  generate(reps = 1000, type = "permute") |> 
  calculate(stat = "diff in props", order = c("metal", "deep-house"))
null_distribution

Response: popular_or_not (factor)
Explanatory: track_genre (factor)
Null Hypothesis: independence
# A tibble: 1,000 × 2
   replicate       stat
       <int>      <dbl>
 1         1  0.0140000
 2         2 -0.0420000
 3         3  0.0220000
 4         4 -0.0140000
 5         5 -0.0180000
 6         6 -0.0160000
 7         7  0.0160000
 8         8 -0.0400000
 9         9  0.0140000
10        10  0.0120000
# ℹ 990 more rows

Observe that we have 1000 values of stat, each representing one instance of $\widehat{p}_{m} - \widehat{p}_{d}$ in a hypothesized world of no difference in genre popularity. Observe as well that we chose the name of this data frame carefully: null_distribution. Recall once again from Section 9.3 that sampling distributions when the null hypothesis $H_0$ is assumed to be true have a special name: the null distribution.

What was the observed difference in popularity rates? In other words, what was the observed test statistic $\widehat{p}_{m} - \widehat{p}_{f}$? Recall from Section 9.2 that we computed this observed difference by hand to be 0.563 - 0.529 = 0.034 = 3.4%. We can also compute this value using the previous infer code but with the hypothesize() and generate() steps removed. Let’s save this in obs_diff_prop:

obs_diff_prop <- spotify_metal_deephouse |> 
  specify(formula = popular_or_not ~ track_genre, success = "popular") |> 
  calculate(stat = "diff in props", order = c("metal", "deep-house"))
obs_diff_prop

Response: popular_or_not (factor)
Explanatory: track_genre (factor)
# A tibble: 1 × 1
       stat
      <dbl>
1 0.0340000

Note that there is also a wrapper function in infer called observe() that can be used to calculate the observed test statistic. However, we chose to use the specify(), calculate(), and hypothesize() functions to help you continue to use the common verbs and build practice with them.

spotify_metal_deephouse |> 
  observe(formula = popular_or_not ~ track_genre, 
          success = "popular", 
          stat = "diff in props", 
          order = c("metal", "deep-house"))

Response: popular_or_not (factor)
Explanatory: track_genre (factor)
# A tibble: 1 × 1
       stat
      <dbl>
1 0.0340000

5. `visualize` the p-value

The final step is to measure how surprised we are by a difference of 3.4% in a hypothesized universe of no difference in genre popularity. If the observed difference of 0.034 is highly unlikely, then we would be inclined to reject the validity of our hypothesized universe.

We start by visualizing the null distribution of our 1000 values of $\widehat{p}_{m} - \widehat{p}_{d}$ using visualize() in Figure 9.8. Recall that these are values of the difference in popularity rates assuming $H_0$ is true. This corresponds to being in our hypothesized universe of no difference in genre popularity.

visualize(null_distribution, bins = 25)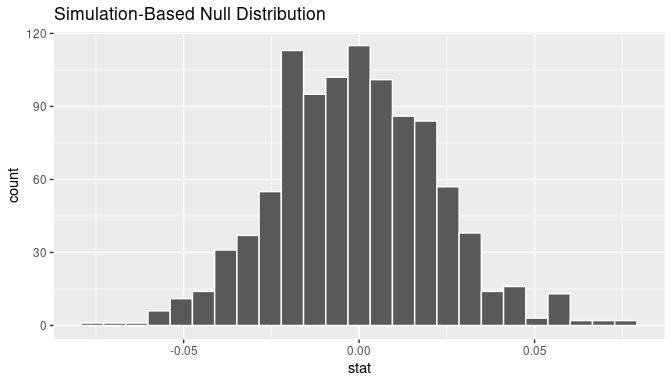

FIGURE 9.8: Null distribution.

Let’s now add what happened in real life to Figure 9.8, the observed difference in popularity rates of 0.563 - 0.529 = 0.034 = 3.4%. However, instead of merely adding a vertical line using geom_vline(), let’s use the shade_p_value() function with obs_stat set to the observed test statistic value we saved in obs_diff_prop.

Furthermore, we will set the direction = "right" reflecting our alternative hypothesis $H_A: p_{m} - p_{d} > 0$. Recall our alternative hypothesis $H_A$ is that $p_{m} - p_{d} > 0$, stating that there is a difference in popularity rates in favor of metal songs. “More extreme” here corresponds to differences that are “bigger” or “more positive” or “more to the right.” Hence we set the direction argument of shade_p_value() to be "right".

On the other hand, had our alternative hypothesis $H_A$ been the other possible one-sided alternative $p_{m} - p_{d} < 0$, suggesting popularity in favor of deep house songs, we would have set direction = "left". Had our alternative hypothesis $H_A$ been two-sided $p_{m} - p_{d} \neq 0$, suggesting discrimination in either direction, we would have set direction = "both".

visualize(null_distribution, bins = 25) + 
  shade_p_value(obs_stat = obs_diff_prop, direction = "right")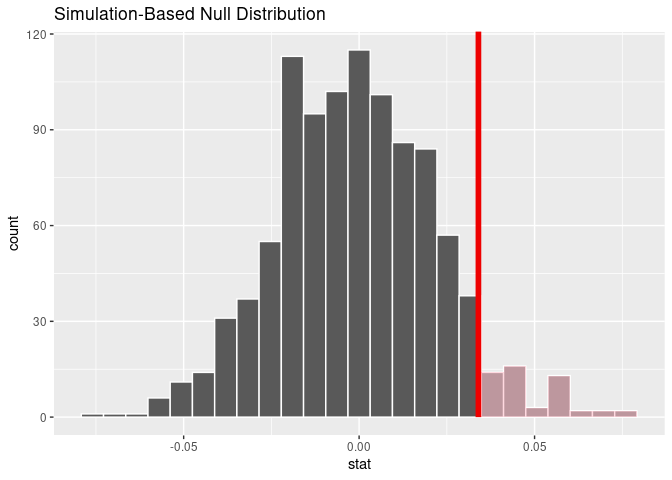

FIGURE 9.9: Shaded histogram to show $p$-value.

In the resulting Figure 9.9, the solid dark line marks 0.034 = 3.4%. However, what does the shaded-region correspond to? This is the $p$-value. Recall the definition of the $p$-value from Section 9.3:

A $p$-value is the probability of obtaining a test statistic just as or more extreme than the observed test statistic assuming the null hypothesis $H_0$ is true.

So judging by the shaded region in Figure 9.9, it seems we would somewhat rarely observe differences in popularity rates of 0.034 = 3.4% or more in a hypothesized universe of no difference in genre popularity. In other words, the $p$-value is somewhat small. Hence, we would be inclined to reject this hypothesized universe, or using statistical language we would “reject $H_0$.”

What fraction of the null distribution is shaded? In other words, what is the exact value of the $p$-value? We can compute it using the get_p_value() function with the same arguments as the previous shade_p_value() code:

null_distribution |> 
  get_p_value(obs_stat = obs_diff_prop, direction = "right")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.065

Keeping the definition of a $p$-value in mind, the probability of observing a difference in popularity rates as large as 0.034 = 3.4% due to sampling variation alone in the null distribution is 0.065 = 6.5%. Since this $p$-value is smaller than our pre-specified significance level $\alpha$ = 0.1, we reject the null hypothesis $H_0: p_{m} - p_{d} = 0$. In other words, this $p$-value is sufficiently small to reject our hypothesized universe of no difference in genre popularity. We instead have enough evidence to change our mind in favor of difference in genre popularity being a likely culprit here. Observe that whether we reject the null hypothesis $H_0$ or not depends in large part on our choice of significance level $\alpha$. We will discuss this more in Subsection 9.5.3.

9.4.2 Comparison with confidence intervals

One of the great things about the infer package is that we can jump seamlessly between conducting hypothesis tests and constructing confidence intervals with minimal changes! Recall the code from the previous section that creates the null distribution, which in turn is needed to compute the $p$-value:

null_distribution <- spotify_metal_deephouse |> 
  specify(formula = popular_or_not ~ track_genre, success = "popular") |> 
  hypothesize(null = "independence") |> 
  generate(reps = 1000, type = "permute") |> 
  calculate(stat = "diff in props", order = c("metal", "deep-house"))

To create the corresponding bootstrap distribution needed to construct a 90% confidence interval for $p_{m} - p_{d}$, we only need to make two changes. First, we remove the hypothesize() step since we are no longer assuming a null hypothesis $H_0$ is true. We can do this by deleting or commenting out the hypothesize() line of code. Second, we switch the type of resampling in the generate() step to be "bootstrap" instead of "permute".

bootstrap_distribution <- spotify_metal_deephouse |> 
  specify(formula = popular_or_not ~ track_genre, success = "popular") |> 
  # Change 1 - Remove hypothesize():
  # hypothesize(null = "independence") |> 
  # Change 2 - Switch type from "permute" to "bootstrap":
  generate(reps = 1000, type = "bootstrap") |> 
  calculate(stat = "diff in props", order = c("metal", "deep-house"))

Using this bootstrap_distribution, let’s first compute the percentile-based confidence intervals, as we did in Section 8.2.2:

percentile_ci <- bootstrap_distribution |> 
  get_confidence_interval(level = 0.90, type = "percentile")
percentile_ci

# A tibble: 1 × 2
     lower_ci  upper_ci
        <dbl>     <dbl>
1 0.000355780 0.0701690

Using our shorthand interpretation for 90% confidence intervals, we are 90% “confident” that the true difference in population proportions $p_{m} - p_{d}$ is between (0, 0.07). Let’s visualize bootstrap_distribution and this percentile-based 90% confidence interval for $p_{m} - p_{d}$ in Figure 9.10.

visualize(bootstrap_distribution) + 
  shade_confidence_interval(endpoints = percentile_ci)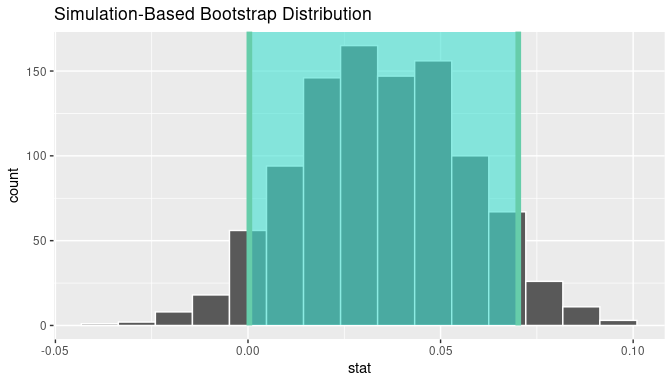

$Percentile-based 95\% confidence interval.$

FIGURE 9.10: Percentile-based 95% confidence interval.

Notice a key value that is not included in the 95% confidence interval for $p_{m} - p_{d}$: the value 0 (but just barely!). In other words, a difference of 0 is not included in our net, suggesting that $p_{m}$ and $p_{d}$ are truly different! Furthermore, observe how the entirety of the 95% confidence interval for $p_{m} - p_{d}$ lies above 0, suggesting that this difference is in favor of metal.

Learning check

(LC9.1) Why does the following code produce an error? In other words, what about the response and predictor variables make this not a possible computation with the infer package?

library(moderndive)
library(infer)
null_distribution_mean <- spotify_metal_deephouse |>
  specify(formula = popular_or_not ~ track_genre, success = "popular") |> 
  hypothesize(null = "independence") |> 
  generate(reps = 1000, type = "permute") |> 
  calculate(stat = "diff in means", order = c("metal", "deep-house"))

(LC9.2) Why are we relatively confident that the distributions of the sample proportions will be good approximations of the population distributions of popularity proportions for the two genres?

(LC9.3) Using the definition of p-value, write in words what the $p$-value represents for the hypothesis test comparing the popularity rates for metal and deep house.

9.4.3 There is only one test

Let’s recap the steps necessary to conduct a hypothesis test using the terminology, notation, and definitions related to sampling you saw in Section 9.3 and the infer workflow from Subsection 9.4.1:

specify() the variables of interest in your data frame.
hypothesize() the null hypothesis $H_0$. In other words, set a “model for the universe” assuming $H_0$ is true.
generate() shuffles assuming $H_0$ is true. In other words, simulate data assuming $H_0$ is true.
calculate() the test statistic of interest, both for the observed data and your simulated data.
visualize() the resulting null distribution and compute the $p$-value by comparing the null distribution to the observed test statistic.

While this is a lot to digest, especially the first time you encounter hypothesis testing, the nice thing is that once you understand this general framework, then you can understand any hypothesis test. In a famous blog post, computer scientist Allen Downey called this the “There is only one test” framework, for which he created the flowchart displayed in Figure 9.11.

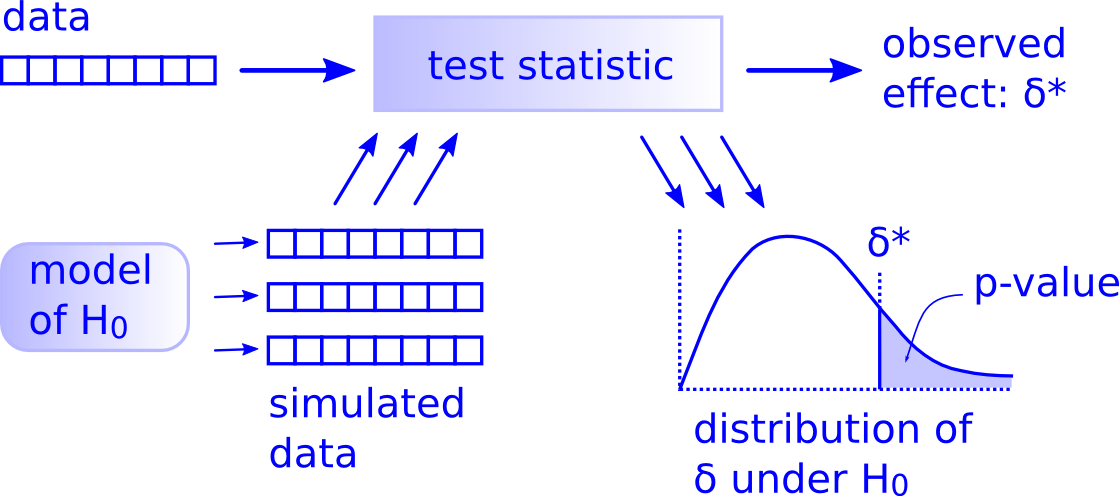
FIGURE 9.11: Allen Downey’s hypothesis testing framework.

Notice its similarity with the “hypothesis testing with infer” diagram you saw in Figure 9.7. That is because the infer package was explicitly designed to match the “There is only one test” framework. So if you can understand the framework, you can easily generalize these ideas for all hypothesis-testing scenarios. Whether for population proportions $p$, population means $\mu$, differences in population proportions $p_1 - p_2$, differences in population means $\mu_1 - \mu_2$, and as you will see in Chapter 10 on inference for regression, population regression slopes $\beta_1$ as well. In fact, it applies more generally even than just these examples to more complicated hypothesis tests and test statistics as well.

Learning check

(LC9.4) Describe in a paragraph how we used Allen Downey’s diagram to conclude if a statistical difference existed between the popularity rate of metal and deep house for the Spotify example.

9.5 Interpreting hypothesis tests

Interpreting the results of hypothesis tests is one of the more challenging aspects of this method for statistical inference. In this section, we will focus on ways to help with deciphering the process and address some common misconceptions.

9.5.1 Two possible outcomes

In Section 9.3, we mentioned that given a pre-specified significance level $\alpha$ there are two possible outcomes of a hypothesis test:

If the $p$-value is less than $\alpha$, then we reject the null hypothesis $H_0$ in favor of $H_A$.
If the $p$-value is greater than or equal to $\alpha$, we fail to reject the null hypothesis $H_0$.

Unfortunately, the latter result is often misinterpreted as “accepting the null hypothesis $H_0$.” While at first glance it may seem that the statements “failing to reject $H_0$” and “accepting $H_0$” are equivalent, there actually is a subtle difference. Saying that we “accept the null hypothesis $H_0$” is equivalent to stating that “we think the null hypothesis $H_0$ is true.” However, saying that we “fail to reject the null hypothesis $H_0$” is saying something else: “While $H_0$ might still be false, we do not have enough evidence to say so.” In other words, there is an absence of enough proof. However, the absence of proof is not proof of absence.

To further shed light on this distinction, let’s use the United States criminal justice system as an analogy. A criminal trial in the United States is a similar situation to hypothesis tests whereby a choice between two contradictory claims must be made about a defendant who is on trial:

The defendant is truly either “innocent” or “guilty.”
The defendant is presumed “innocent until proven guilty.”
The defendant is found guilty only if there is strong evidence that the defendant is guilty. The phrase “beyond a reasonable doubt” is often used as a guideline for determining a cutoff for when enough evidence exists to find the defendant guilty.
The defendant is found to be either “not guilty” or “guilty” in the ultimate verdict.

In other words, not guilty verdicts are not suggesting the defendant is innocent, but instead that “while the defendant may still actually be guilty, there was not enough evidence to prove this fact.” Now let’s make the connection with hypothesis tests:

Either the null hypothesis $H_0$ or the alternative hypothesis $H_A$ is true.
Hypothesis tests are conducted assuming the null hypothesis $H_0$ is true.
We reject the null hypothesis $H_0$ in favor of $H_A$ only if the evidence found in the sample suggests that $H_A$ is true. The significance level $\alpha$ is used as a guideline to set the threshold on just how strong of evidence we require.
We ultimately decide to either “fail to reject $H_0$” or “reject $H_0$.”

So while gut instinct may suggest “failing to reject $H_0$” and “accepting $H_0$” are equivalent statements, they are not. “Accepting $H_0$” is equivalent to finding a defendant innocent. However, courts do not find defendants “innocent,” but rather they find them “not guilty.” Putting things differently, defense attorneys do not need to prove that their clients are innocent, rather they only need to prove that clients are not “guilty beyond a reasonable doubt.”

So going back to our songs activity in Section 9.4, recall that our hypothesis test was $H_0: p_{m} - p_{d} = 0$ versus $H_A: p_{m} - p_{d} > 0$ and that we used a pre-specified significance level of $\alpha$ = 0.1. We found a $p$-value of 0.065. Since the $p$-value was smaller than $\alpha$ = 0.1, we rejected $H_0$. In other words, we found needed levels of evidence in this particular sample to say that $H_0$ is false at the $\alpha$ = 0.1 significance level. We also state this conclusion using non-statistical language: we found enough evidence in this data to suggest that there was a difference in the popularity of our two genres of music.

9.5.2 Types of errors

Unfortunately, there is some chance a jury or a judge can make an incorrect decision in a criminal trial by reaching the wrong verdict. For example, finding a truly innocent defendant “guilty.” Or on the other hand, finding a truly guilty defendant “not guilty.” This can often stem from the fact that prosecutors do not have access to all the relevant evidence, but instead are limited to whatever evidence the police can find.

The same holds for hypothesis tests. We can make incorrect decisions about a population parameter because we only have a sample of data from the population and thus sampling variation can lead us to incorrect conclusions.

There are two possible erroneous conclusions in a criminal trial: either (1) a truly innocent person is found guilty or (2) a truly guilty person is found not guilty. Similarly, there are two possible errors in a hypothesis test: either (1) rejecting $H_0$ when in fact $H_0$ is true, called a Type I error or (2) failing to reject $H_0$ when in fact $H_0$ is false, called a Type II error. Another term used for “Type I error” is “false positive,” while another term for “Type II error” is “false negative.”

This risk of error is the price researchers pay for basing inference on a sample instead of performing a census on the entire population. But as we have seen in our numerous examples and activities so far, censuses are often very expensive and other times impossible, and thus researchers have no choice but to use a sample. Thus in any hypothesis test based on a sample, we have no choice but to tolerate some chance that a Type I error will be made and some chance that a Type II error will occur.

To help understand the concepts of Type I error and Type II errors, we apply these terms to our criminal justice analogy in Figure 9.12.

FIGURE 9.12: Type I and Type II errors in criminal trials.

Thus, a Type I error corresponds to incorrectly putting a truly innocent person in jail, whereas a Type II error corresponds to letting a truly guilty person go free. Let’s show the corresponding table in Figure 9.13 for hypothesis tests.

FIGURE 9.13: Type I and Type II errors in hypothesis tests.

9.5.3 How do we choose alpha?

If we are using a sample to make inferences about a population, we are operating under uncertainty and run the risk of making statistical errors. These are not errors in calculations or in the procedure used, but errors in the sense that the sample used may lead us to construct a confidence interval that does not contain the true value of the population parameter, for example. In the case of hypothesis testing, there are two well-defined errors: a Type I and a Type II error:

A Type I Error is rejecting the null hypothesis when it is true. The probability of a Type I Error occurring is $\alpha$, the significance level, which we defined in Subsection 9.1.1 and in Section 9.3
A Type II Error is failing to reject the null hypothesis when it is false. The probability of a Type II Error is denoted by $\beta$. The value of $1-\beta$ is known as the power of the test.

Ideally, we would like to minimize the errors, and we would like $\alpha = 0$ and $\beta = 0$. However, this is not possible as there will always be the possibility of committing one of these error when making a decision based on sample data. Furthermore, these two error probabilities are inversely related. As the probability of a Type I error goes down, the probability of a Type II error goes up.

When constructing a hypothesis test, we have control of the probability of committing a Type I Error because we can decide what is the significance level $\alpha$ we want to use. Once $\alpha$ has been pre-specified, we try to minimize $\beta$, the fraction of incorrect non-rejections of the null hypothesis.

So for example if we used $\alpha$ = 0.01, we would be using a hypothesis testing procedure that in the long run would incorrectly reject the null hypothesis $H_0$ one percent of the time. This is analogous to setting the confidence level of a confidence interval.

So what value should you use for $\alpha$? While different fields of study have adopted different conventions, although $\alpha = 0.05$ is perhaps the most popular threshold, there is nothing special about this or any other number. Please review Subsection 9.1.1 and our discussion about $\alpha$ and our tolerance for uncertainty. In addition, observe that choosing a relatively small value of $\alpha$ reduces our chances of rejecting the null hypothesis, and also of committing a Type I Error; but increases the probability of committing a Type II Error.

On the other hand, choosing a relatively large value of $\alpha$ increases the chances of failing to reject the null hypothesis, and also of committing a Type I Error; but reduces the probability of committing a Type II Error. Depending on the problem at hand, we may be willing to have a larger significance level in certain scenarios and a smaller significance level in others.

Learning check

(LC9.5) What is wrong about saying, “The defendant is innocent.” based on the US system of criminal trials?

(LC9.6) What is the purpose of hypothesis testing?

(LC9.7) What are some flaws with hypothesis testing? How could we alleviate them?

(LC9.8) Consider two $\alpha$ significance levels of 0.1 and 0.01. Of the two, which would lead to a higher chance of committing a Type I Error?

9.6 Case study: are action or romance movies rated higher?

Let’s apply our knowledge of hypothesis testing to answer the question: “Are action or romance movies rated higher on IMDb?”. IMDb is a database on the internet providing information on movie and television show casts, plot summaries, trivia, and ratings. We will investigate if, on average, action or romance movies get higher ratings on IMDb.

9.6.1 IMDb ratings data

The movies dataset in the ggplot2movies package contains information on 58,788 movies that have been rated by users of IMDb.com.

movies

# A tibble: 58,788 × 24
   title        year length budget rating votes    r1    r2    r3    r4    r5    r6    r7    r8    r9   r10 mpaa  Action
   <chr>       <int>  <int>  <int>  <dbl> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>  <int>
 1 $            1971    121     NA    6.4   348   4.5   4.5   4.5   4.5  14.5  24.5  24.5  14.5   4.5   4.5 ""         0
 2 $1000 a To…  1939     71     NA    6      20   0    14.5   4.5  24.5  14.5  14.5  14.5   4.5   4.5  14.5 ""         0
 3 $21 a Day …  1941      7     NA    8.2     5   0     0     0     0     0    24.5   0    44.5  24.5  24.5 ""         0
 4 $40,000      1996     70     NA    8.2     6  14.5   0     0     0     0     0     0     0    34.5  45.5 ""         0
 5 $50,000 Cl…  1975     71     NA    3.4    17  24.5   4.5   0    14.5  14.5   4.5   0     0     0    24.5 ""         0
 6 $pent        2000     91     NA    4.3    45   4.5   4.5   4.5  14.5  14.5  14.5   4.5   4.5  14.5  14.5 ""         0
 7 $windle      2002     93     NA    5.3   200   4.5   0     4.5   4.5  24.5  24.5  14.5   4.5   4.5  14.5 "R"        1
 8 '15'         2002     25     NA    6.7    24   4.5   4.5   4.5   4.5   4.5  14.5  14.5  14.5   4.5  14.5 ""         0
 9 '38          1987     97     NA    6.6    18   4.5   4.5   4.5   0     0     0    34.5  14.5   4.5  24.5 ""         0
10 '49-'17      1917     61     NA    6      51   4.5   0     4.5   4.5   4.5  44.5  14.5   4.5   4.5   4.5 ""         0
# ℹ 58,778 more rows
# ℹ 6 more variables: Animation <int>, Comedy <int>, Drama <int>, Documentary <int>, Romance <int>, Short <int>

We will focus on a random sample of 68 movies that are classified as either “action” or “romance” movies but not both. We disregard movies that are classified as both so that we can assign all 68 movies into either category. Furthermore, since the original movies dataset was a little messy, we provide a pre-wrangled version of our data in the movies_sample data frame included in the moderndive package. If you are curious, you can look at the necessary data-wrangling code to do this on GitHub.

movies_sample

# A tibble: 68 × 4
   title                     year rating genre  
   <chr>                    <int>  <dbl> <chr>  
 1 Underworld                1985    3.1 Action 
 2 Love Affair               1932    6.3 Romance
 3 Junglee                   1961    6.8 Romance
 4 Eversmile, New Jersey     1989    5   Romance
 5 Search and Destroy        1979    4   Action 
 6 Secreto de Romelia, El    1988    4.9 Romance
 7 Amants du Pont-Neuf, Les  1991    7.4 Romance
 8 Illicit Dreams            1995    3.5 Action 
 9 Kabhi Kabhie              1976    7.7 Romance
10 Electric Horseman, The    1979    5.8 Romance
# ℹ 58 more rows

The variables include the title and year the movie was filmed. Furthermore, we have a numerical variable rating, which is the IMDb rating out of 10 stars, and a binary categorical variable genre indicating if the movie was an Action or Romance movie. We are interested in whether Action or Romance movies got a higher rating on average.

Let’s perform an exploratory data analysis of this data. Recall from Subsection 2.7.1 that a boxplot is a visualization we can use to show the relationship between a numerical and a categorical variable. Another option you saw in Section 2.6 would be to use a faceted histogram. However, in the interest of brevity, let’s only present the boxplot in Figure 9.14.

ggplot(data = movies_sample, aes(x = genre, y = rating)) +
  geom_boxplot() +
  labs(y = "IMDb rating")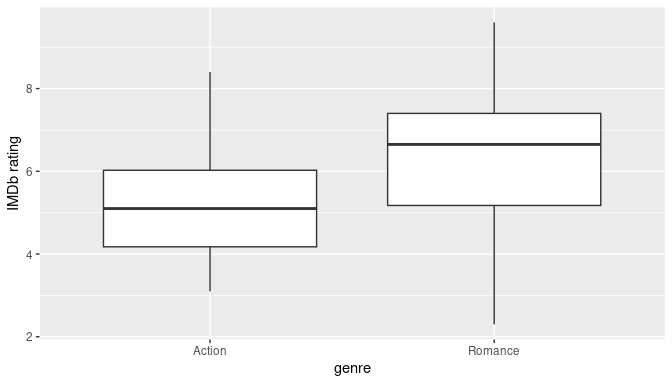

FIGURE 9.14: Boxplot of IMDb rating vs. genre.

Eyeballing Figure 9.14, romance movies have a higher median rating. Do we have reason to believe, however, that there is a significant difference between the mean rating for action movies compared to romance movies? It is hard to say just based on this plot. The boxplot does show that the median sample rating is higher for romance movies.

However, there is a large amount of overlap between the boxes. Recall that the median is not necessarily the same as the mean either, depending on whether the distribution is skewed.

Let’s calculate some summary statistics split by the binary categorical variable genre: the number of movies, the mean rating, and the standard deviation split by genre. We will do this using dplyr data wrangling verbs. Notice in particular how we count the number of each type of movie using the n() summary function.

movies_sample |> 
  group_by(genre) |> 
  summarize(n = n(), mean_rating = mean(rating), std_dev = sd(rating))

# A tibble: 2 × 4
  genre       n mean_rating std_dev
  <chr>   <int>       <dbl>   <dbl>
1 Action     32     5.275   1.36121
2 Romance    36     6.32222 1.60963

Observe that we have 36 movies with an average rating of 6.322 stars and 32 movies with an average rating of 5.275 stars. The difference in these average ratings is thus 6.322 - 5.275 = 1.047. So there appears to be an edge of 1.047 stars in favor of romance movies. The question is, however, are these results indicative of a true difference for all romance and action movies? Or could we attribute this difference to chance sampling variation?

9.6.2 Sampling scenario

Let’s now revisit this study in terms of terminology and notation related to sampling we studied in Subsection 7.2.1. The study population is all movies in the IMDb database that are either action or romance (but not both). The sample from this population is the 68 movies included in the movies_sample dataset.

Since this sample was randomly taken from the population movies, it is representative of all romance and action movies on IMDb. Thus, any analysis and results based on movies_sample can generalize to the entire population. What are the relevant population parameter and point estimates? We introduce the fourth sampling scenario in Table 9.6.

TABLE 9.6: Scenarios of sampling for inference
Scenario	Population parameter	Notation	Point estimate	Symbol(s)
1	Population proportion	$p$	Sample proportion	$\widehat{p}$
2	Population mean	$\mu$	Sample mean	$\overline{x}$ or $\widehat{\mu}$
3	Difference in population proportions	$p_1 - p_2$	Difference in sample proportions	$\widehat{p}_1 - \widehat{p}_2$
4	Difference in population means	$\mu_1 - \mu_2$	Difference in sample means	$\overline{x}_1 - \overline{x}_2$ or $\widehat{\mu}_1 - \widehat{\mu}_2$

So, whereas the sampling bowl exercise in Section 7.1 concerned proportions, the almonds exercise in Section 8.2.1 concerned means, the case study on whether yawning is contagious in Section 8.4 and the music genre activity in Section 9.2 concerned differences in proportions, we are now concerned with differences in means.

In other words, the population parameter of interest is the difference in population mean ratings $\mu_a - \mu_r$, where $\mu_a$ is the mean rating of all action movies on IMDb and similarly $\mu_r$ is the mean rating of all romance movies. Additionally the point estimate/sample statistic of interest is the difference in sample means $\overline{x}_a - \overline{x}_r$, where $\overline{x}_a$ is the mean rating of the $n_a$ = 32 movies in our sample and $\overline{x}_r$ is the mean rating of the $n_r$ = 36 in our sample. Based on our earlier exploratory data analysis, our estimate $\overline{x}_a - \overline{x}_r$ is $5.275 - 6.322 = -1.047$.

So there appears to be a slight difference of -1.047 in favor of romance movies. The question is, however, could this difference of -1.047 be merely due to chance and sampling variation? Or are these results indicative of a true difference in mean ratings for all romance and action movies on IMDb? To answer this question, we will use hypothesis testing.

9.6.3 Conducting the hypothesis test

We will be testing:

\[ \begin{aligned} H_0 &: \mu_a - \mu_r = 0\\ \text{vs } H_A&: \mu_a - \mu_r \neq 0 \end{aligned} \]

In other words, the null hypothesis $H_0$ suggests that both romance and action movies have the same mean rating. This is the “hypothesized universe” we will assume is true. On the other hand, the alternative hypothesis $H_A$ suggests that there is a difference. Unlike the one-sided alternative we used in the popularity exercise $H_A: p_m - p_f > 0$, we are now considering a two-sided alternative of $H_A: \mu_a - \mu_r \neq 0$.

Furthermore, we will pre-specify a low significance level of $\alpha$ = 0.001. By setting this value low, all things being equal, there is a lower chance that the $p$-value will be less than $\alpha$. Thus, there is a lower chance that we will reject the null hypothesis $H_0$ in favor of the alternative hypothesis $H_A$. In other words, we will reject the hypothesis that there is no difference in mean ratings for all action and romance movies, only if we have quite strong evidence. This is known as a “conservative” hypothesis testing procedure.

1. `specify` variables

Let’s now perform all the steps of the infer workflow. We first specify() the variables of interest in the movies_sample data frame using the formula rating ~ genre. This tells infer that the numerical variable rating is the outcome variable, while the binary variable genre is the explanatory variable. Note that unlike previously when we were interested in proportions, since we are now interested in the mean of a numerical variable, we do not need to set the success argument.

movies_sample |> 
  specify(formula = rating ~ genre)

Response: rating (numeric)
Explanatory: genre (factor)
# A tibble: 68 × 2
   rating genre  
    <dbl> <fct>  
 1    3.1 Action 
 2    6.3 Romance
 3    6.8 Romance
 4    5   Romance
 5    4   Action 
 6    4.9 Romance
 7    7.4 Romance
 8    3.5 Action 
 9    7.7 Romance
10    5.8 Romance
# ℹ 58 more rows

Observe at this point that the data in movies_sample has not changed. The only change so far is the newly defined Response: rating (numeric) and Explanatory: genre (factor) meta-data.

2. `hypothesize` the null

We set the null hypothesis $H_0: \mu_a - \mu_r = 0$ by using the hypothesize() function. Since we have two samples, action and romance movies, we set null to be "independence" as we described in Section 9.4.

movies_sample |> 
  specify(formula = rating ~ genre) |> 
  hypothesize(null = "independence")

Response: rating (numeric)
Explanatory: genre (factor)
Null Hypothesis: independence
# A tibble: 68 × 2
   rating genre  
    <dbl> <fct>  
 1    3.1 Action 
 2    6.3 Romance
 3    6.8 Romance
 4    5   Romance
 5    4   Action 
 6    4.9 Romance
 7    7.4 Romance
 8    3.5 Action 
 9    7.7 Romance
10    5.8 Romance
# ℹ 58 more rows

3. `generate` replicates

After we have set the null hypothesis, we generate “shuffled” replicates assuming the null hypothesis is true by repeating the shuffling/permutation exercise you performed in Section 9.2.

We will repeat this resampling without replacement of type = "permute" a total of reps = 1000 times. Feel free to run the code to check out what the generate() step produces.

movies_sample |> 
  specify(formula = rating ~ genre) |> 
  hypothesize(null = "independence") |> 
  generate(reps = 1000, type = "permute") |> 
  View()

4. `calculate` summary statistics

Now that we have 1000 replicated “shuffles” assuming the null hypothesis $H_0$ that both Action and Romance movies on average have the same ratings on IMDb, let’s calculate() the appropriate summary statistic for these 1000 replicated shuffles. From Section 9.3, summary statistics relating to hypothesis testing have a specific name: test statistics. Since the unknown population parameter of interest is the difference in population means $\mu_{a} - \mu_{r}$, the test statistic of interest here is the difference in sample means $\overline{x}_{a} - \overline{x}_{r}$.

For each of our 1000 shuffles, we can calculate this test statistic by setting stat = "diff in means". Furthermore, since we are interested in $\overline{x}_{a} - \overline{x}_{r}$, we set order = c("Action", "Romance"). Let’s save the results in a data frame called null_distribution_movies:

null_distribution_movies <- movies_sample |> 
  specify(formula = rating ~ genre) |> 
  hypothesize(null = "independence") |> 
  generate(reps = 1000, type = "permute") |> 
  calculate(stat = "diff in means", order = c("Action", "Romance"))
null_distribution_movies

# A tibble: 1,000 × 2
   replicate      stat
       <int>     <dbl>
 1         1  0.511111
 2         2  0.345833
 3         3 -0.327083
 4         4 -0.209028
 5         5 -0.433333
 6         6 -0.102778
 7         7  0.387153
 8         8  0.168750
 9         9  0.257292
10        10  0.334028
# ℹ 990 more rows

Observe that we have 1000 values of stat, each representing one instance of $\overline{x}_{a} - \overline{x}_{r}$. The 1000 values form the null distribution, which is the technical term for the sampling distribution of the difference in sample means $\overline{x}_{a} - \overline{x}_{r}$ assuming $H_0$ is true. What happened in real life? What was the observed difference in popularity rates? What was the observed test statistic $\overline{x}_{a} - \overline{x}_{r}$? Recall from our earlier data wrangling, this observed difference in means was $5.275 - 6.322 = -1.047$. We can also achieve this using the code that constructed the null distribution null_distribution_movies but with the hypothesize() and generate() steps removed. We save this in obs_diff_means:

obs_diff_means <- movies_sample |> 
  specify(formula = rating ~ genre) |> 
  calculate(stat = "diff in means", order = c("Action", "Romance"))
obs_diff_means

Response: rating (numeric)
Explanatory: genre (factor)
# A tibble: 1 × 1
      stat
     <dbl>
1 -1.04722

5. `visualize` the p-value

Lastly, in order to compute the $p$-value, we have to assess how “extreme” the observed difference in means of -1.047 is. We do this by comparing -1.047 to our null distribution, which was constructed in a hypothesized universe of no true difference in movie ratings. We visualize both the null distribution and the $p$-value in Figure 9.15. Unlike our example in Subsection 9.4.1 involving music popularity, since we have a two-sided $H_A: \mu_a - \mu_r \neq 0$, we have to allow for both possibilities for more extreme, so we set direction = "both".

visualize(null_distribution_movies, bins = 10) + 
  shade_p_value(obs_stat = obs_diff_means, direction = "both")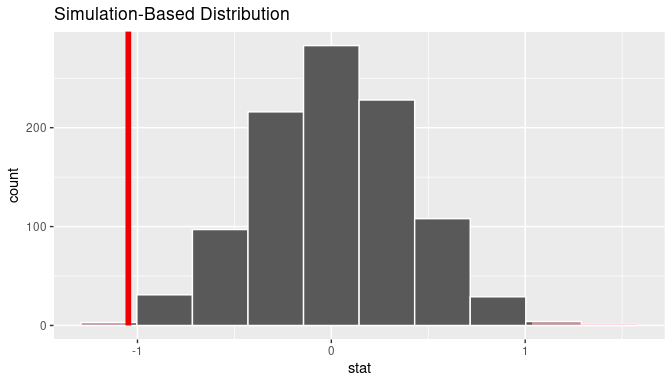

FIGURE 9.15: Null distribution, observed test statistic, and $p$-value.

Let’s go over the elements of this plot. First, the histogram is the null distribution. Second, the solid line is the observed test statistic, or the difference in sample means we observed in real life of $5.275 - 6.322 = -1.047$. Third, the two shaded areas of the histogram form the $p$-value, or the probability of obtaining a test statistic just as or more extreme than the observed test statistic assuming the null hypothesis $H_0$ is true.

What proportion of the null distribution is shaded? In other words, what is the numerical value of the $p$-value? We use the get_p_value() function to compute this value:

null_distribution_movies |> 
  get_p_value(obs_stat = obs_diff_means, direction = "both")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.004

This $p$-value of 0.004 is very small. In other words, there is a very small chance that we would observe a difference of 5.275 - 6.322 = -1.047 in a hypothesized universe where there was truly no difference in ratings.

But this $p$-value is larger than our (even smaller) pre-specified $\alpha$ significance level of 0.001. Thus, we are inclined to fail to reject the null hypothesis $H_0: \mu_a - \mu_r = 0$. In non-statistical language, the conclusion is: we do not have the evidence needed in this sample of data to suggest that we should reject the hypothesis that there is no difference in mean IMDb ratings between romance and action movies. We, thus, cannot say that a difference exists in romance and action movie ratings, on average, for all IMDb movies.

Learning check

(LC9.9) Conduct the same analysis comparing action movies versus romantic movies using the median rating instead of the mean rating. What was different and what was the same?

(LC9.10) What conclusions can you make from viewing the faceted histogram looking at rating versus genre that you could not see when looking at the boxplot?

(LC9.11) Describe in a paragraph how we used Allen Downey’s diagram to conclude if a statistical difference existed between mean movie ratings for action and romance movies.

(LC9.12) Why are we relatively confident that the distributions of the sample ratings will be good approximations of the population distributions of ratings for the two genres?

(LC9.13) Using the definition of $p$-value, write in words what the $p$-value represents for the hypothesis test comparing the mean rating of romance to action movies.

(LC9.14) What is the value of the $p$-value for the two-sided hypothesis test comparing the mean rating of romance to action movies?

(LC9.15) Test your data-wrangling knowledge and EDA skills:

Use dplyr and tidyr to create the necessary data frame focused on only action and romance movies (but not both) from the movies data frame in the ggplot2movies package.
Make a boxplot and a faceted histogram of this population data comparing ratings of action and romance movies from IMDb.
Discuss how these plots compare to the similar plots produced for the movies_sample data.

9.7 Summary and Final Remarks

9.7.1 Theory-based approach for two-sample hypothesis tests

As we did previously when we discussed the theory-based approach for confidence intervals or hypothesis tests for the one-sample problem, we discuss now some of the theory needed to perform two-sample hypothesis tests. We present an example of a traditional theory-based method to conduct hypothesis tests. This method relies on the Central Limit Theorem and properties of random variables, expected value, variance, and standard deviation. It is also a direct extension of the one-sample problem discussed in Section 9.1.

Theory-based methods have been used for decades when researchers did not have access to computers that could run thousands of calculations quickly and efficiently. Now computing power is more accessible and simulation-based methods are becoming more popular, but researchers in many fields continue to use theory-based methods.

The theory-based method we focus on is known as the Welch’s two-sample $t$-test for testing differences in sample means. The test statistic we use is the two-sample $t$-statistic, a standardized version of the difference in sample means $\overline{x}_1 - \overline{x}_2$. The data we use is once again the movies_sample data of action and romance movies from Section 9.6.

Welch’s two-sample t-statistic

In Section 7.5 we introduced the sampling distribution for the difference of two sample means. If we let $\overline X_a$ be the random variable for the sample mean of action films’ rating and $\overline X_r$ the one for romance film’s rating, the distribution of the difference of these random variables is

\[\overline X_a - \overline X_r \sim Normal \left(\mu_a - \mu_r, \sqrt{\frac{\sigma_a^2}{n_a} + \frac{\sigma^2_r}{n_r}} \right)\]

where $\mu_a$ and $\mu_r$ are the population mean ratings, $\sigma_a$ and $\sigma_r$ the population standard deviations, and $n_a$ and $n_r$ the sample sizes for action and romance genres, respectively.

When using the samples, as we did for one-sample problems, we standardize the difference in sample means, $\overline{x}_a - \overline{x}_r$, by subtracting its mean (the differences in population means) and dividing by its standard error. This construct a test statistic known as the Welch’s two-sample $t$-test statistic:

\[t = \dfrac{ (\bar{x}_a - \bar{x}_r) - (\mu_a - \mu_r)}{ \text{SE}(\bar{x}_a - \bar{x}_r) } = \dfrac{ (\bar{x}_a - \bar{x}_r) - (\mu_a - \mu_r)}{ \sqrt{\dfrac{{s_a}^2}{n_a} + \dfrac{{s_r}^2}{n_r}} }\]

Observe that the formula for $\text{SE}(\bar{x}_a - \bar{x}_r)$ has the sample sizes $n_a$ and $n_r$ in them. So as the sample sizes increase, the standard error goes down. We have seen this characteristic for one-sample problems in Subsections 7.3.4 and 7.4.5 when describing the sample distribution of the sample mean or the sample proportion and in Section 8.1 when discussing the sample size effect on confidence intervals.

Let’s state the null and alternative hypotheses for this test:

\[\begin{aligned}&H_0: &\mu_a - \mu_r = 0\\&H_A: &\mu_a - \mu_r \ne 0\end{aligned}\]

The claim under the null hypothesis is that the difference between the population means is zero. This is equivalent to claiming that the means are the same, $\mu_a = \mu_r$, which is the typical test, as we try to determine whether or not the population means are different. Yet, the structure of the test allows for testing other differences as well, if needed.

The Welch’s two-sample $t$-test becomes:

\[t = \dfrac{ (\bar{x}_a - \bar{x}_r) - 0}{ \sqrt{\dfrac{{s_a}^2}{n_a} + \dfrac{{s_r}^2}{n_r}} } = \dfrac{ \bar{x}_a - \bar{x}_r}{ \sqrt{\dfrac{{s_a}^2}{n_a} + \dfrac{{s_r}^2}{n_r}} }\]

Using results based on the Central Limit Theorem, linear combinations of independent random variables, and properties of the expected value, variance, and standard deviation, it can be shown that the Welch’s test statistic follows a $t$ distribution.

In Section 8.1.4 we have discussed the properties of the $t$ distribution and in Figure 8.7 we have shown different $t$ distributions with different degrees of freedom. Recall that the $t$ distribution is similar to the standard normal; its density curve is also bell-shaped, and it is symmetric around zero, but the tails of the $t$ distribution are a little thicker (or heavier) than those of the standard normal. This is important for hypothesis testing, since the $p$-value is calculated from the areas on those tails. Also recall that as the degrees of freedom increase, the $t$-distribution more and more approximates the standard normal curve.

In terms of the Welch’s two-sample $t$-test, it has been shown that the test statistics follows a $t$ distribution with degrees of freedom that can be approximated by

\[ \widehat{df} = \left( \dfrac{s_a^2}{n_a} + \dfrac{s_r^2}{n_r} \right)^2 \Bigg/ \left( \dfrac{\left( \dfrac{s_a^2}{n_a} \right)^2}{n_a - 1} + \dfrac{\left( \dfrac{s_r^2}{n_r} \right)^2}{n_r - 1} \right) \]

This formula is just too long to enter manually every time that is needed. (A suitable approximation for the degrees of freedom using $n_a + n_r - 2$ is often used instead for reasonably large sample sizes.) But, fortunately, R and other statistical software have already done the formula inputting for us by introducing relevant functions. While it is important to get good approximations to the degrees of freedom in order to get the appropriate $p$-values, learning this formula goes beyond the reach of those new to statistical inference, and it does little to build the intuition of the $t$-test. Therefore, we will trust the results that R or other statistical packages provide for us.

Let’s compute the $t$-test statistic. Recall the summary statistics we computed during our exploratory data analysis in Section 9.6.1.

movies_sample |> 
  group_by(genre) |> 
  summarize(n = n(), mean_rating = mean(rating), std_dev = sd(rating))

# A tibble: 2 × 4
  genre       n mean_rating std_dev
  <chr>   <int>       <dbl>   <dbl>
1 Action     32     5.275   1.36121
2 Romance    36     6.32222 1.60963

Using these values, the observed two-sample $t$-test statistic is

\[ \dfrac{ \bar{x}_a - \bar{x}_r}{ \sqrt{\dfrac{{s_a}^2}{n_a} + \dfrac{{s_r}^2}{n_r}} } = \dfrac{5.28 - 6.32}{ \sqrt{\dfrac{{1.36}^2}{32} + \dfrac{{1.61}^2}{36}} } = -2.906 \]

How can we compute the $p$-value using this theory-based test statistic? We could do it by calculating the degrees of freedom and using the function pt() as we did earlier. Instead, we use the function t_test() from the package infer with the appropriate formula and order, as we did for the simulation-based approach.

The results are shown next:

movies_sample |>
  t_test(formula = rating ~ genre, 
         order = c("Action", "Romance"), 
         alternative = "two-sided")

# A tibble: 1 × 7
  statistic    t_df    p_value alternative estimate lower_ci  upper_ci
      <dbl>   <dbl>      <dbl> <chr>          <dbl>    <dbl>     <dbl>
1  -2.90589 65.8496 0.00498319 two.sided   -1.04722 -1.76677 -0.327671

Based on the $p$-value = 0.005 we reject the null hypothesis, the average rating for the Romance movies is not the same as the average rating for the Action movies. This result is similar to the one calculated using the simulation-based approach.

To be able to use the Welch’s $t$-test, there are some conditions that are necessary so that the underlying mathematical theory holds:

The populations should be close to normal or the samples should be large. Many textbooks suggest the sample sizes to be greater than 30, but there is no clear mathematical foundation for this rule of thumb. In general, as long as the distribution of the samples appear to be close to symmetric, the Welch’s $t$-test may provide useful results.
The samples should be random samples.
The sample of one population should be independent from the sample of the other population.

Let’s see if these conditions hold for our movies_sample data:

This is met since $n_a$ = 32 and $n_r$ = 36 do not seem to be highly skewed and therefore are somewhat symmetric.
This is met since we sampled the action and romance movies at random and in an unbiased fashion from the database of all IMDb movies.
Unfortunately, we do not know how IMDb computes the ratings. For example, if the same person can rate multiple movies, then those observations may be related. This does not appear to be a major problem in this context though.

Assuming all three conditions are not clearly broken, we can be reasonably certain that the theory-based $t$-test results are valid.

9.7.2 When inference is not needed

We have now walked through several different examples of how to use the infer package to perform statistical inference: constructing confidence intervals and conducting hypothesis tests. For each of these examples, we made it a point to always perform an exploratory data analysis (EDA) first; specifically, by looking at the raw data values, by using data visualization with ggplot2, and by data wrangling with dplyr beforehand. We highly encourage you to always do the same. As a beginner to statistics, EDA helps you develop intuition as to what statistical methods like confidence intervals and hypothesis tests can tell us. Even as a seasoned practitioner of statistics, EDA helps guide your statistical investigations. In particular, is statistical inference even needed?

Let’s consider an example. Say we are interested in the following question: Of all flights leaving a New York City airport, are Hawaiian Airlines flights in the air for longer than Alaska Airlines flights? Furthermore, let’s assume that 2023 flights are a representative sample of all such flights. Then we can use the flights data frame in the nycflights23 package we introduced in Section 1.4 to answer our question. Let’s filter this data frame to only include Hawaiian and Alaska Airlines using their carrier codes HA and AS:

flights_sample <- flights |> 
  filter(carrier %in% c("HA", "AS"))

There are two possible statistical inference methods we could use to answer such questions. First, we could construct a 95% confidence interval for the difference in population means $\mu_{HA} - \mu_{AS}$, where $\mu_{HA}$ is the mean air time of all Hawaiian Airlines flights and $\mu_{AS}$ is the mean air time of all Alaska Airlines flights. We could then check if the entirety of the interval is greater than 0, suggesting that $\mu_{HA} - \mu_{AS} > 0$, or, in other words suggesting that $\mu_{HA} > \mu_{AS}$. Second, we could perform a hypothesis test of the null hypothesis $H_0: \mu_{HA} - \mu_{AS} = 0$ versus the alternative hypothesis $H_A: \mu_{HA} - \mu_{AS} > 0$.

However, let’s first construct an exploratory visualization as we suggested earlier. Since air_time is numerical and carrier is categorical, a boxplot can display the relationship between these two variables, which we display in Figure 9.16.

ggplot(data = flights_sample, mapping = aes(x = carrier, y = air_time)) +
  geom_boxplot() +
  labs(x = "Carrier", y = "Air Time")

FIGURE 9.16: Air time for Hawaiian and Alaska Airlines flights departing NYC in 2023.

This is what we like to call “no PhD in Statistics needed” moments. You do not have to be an expert in statistics to know that Alaska Airlines and Hawaiian Airlines have notably different air times. The two boxplots do not even overlap! Constructing a confidence interval or conducting a hypothesis test would frankly not provide much more insight than Figure 9.16.

Let’s investigate why we observe such a clear-cut difference between these two airlines using data wrangling. Let’s first group the rows of flights_sample not only by carrier but also by destination dest. Subsequently, we will compute two summary statistics: the number of observations using n() and the mean airtime:

flights_sample |> 
  group_by(carrier, dest) |> 
  summarize(n = n(), mean_time = mean(air_time, na.rm = TRUE), .groups = "keep")

# A tibble: 8 × 4
# Groups:   carrier, dest [8]
  carrier dest      n mean_time
  <chr>   <chr> <int>     <dbl>
1 AS      LAS       1   299    
2 AS      LAX     980   323.929
3 AS      PDX     710   326.383
4 AS      PSP      18   309.611
5 AS      SAN    1034   325.457
6 AS      SEA    2417   324.787
7 AS      SFO    2683   343.542
8 HA      HNL     366   623.287

It turns out that from New York City in 2023 Alaska flew to seven different airports on the West Coast region of the US while Hawaiian only flew to HNL (Honolulu) from NYC. Given the clear difference in distance from New York City to the West Coast versus New York City to Honolulu, it is not surprising that we observe such different (statistically significantly different, in fact) air times in flights.

This is a clear example of not needing to do anything more than a simple exploratory data analysis using data visualization and descriptive statistics to get an appropriate conclusion. This is why we highly recommend you perform an EDA of any sample data before running statistical inference methods like confidence intervals and hypothesis tests.

9.7.3 Problems with p-values

On top of the many common misunderstandings about hypothesis testing and $p$-values we listed in Section 9.5, another unfortunate consequence of the expanded use of $p$-values and hypothesis testing is a phenomenon known as “p-hacking.” p-hacking is the act of “cherry-picking” only results that are “statistically significant” while dismissing those that are not, even if at the expense of the scientific ideas. There are lots of articles written recently about misunderstandings and the problems with $p$-values. We encourage you to check some of them out:

Such issues were getting so problematic that the American Statistical Association (ASA) put out a statement in 2016 titled, “The ASA Statement on Statistical Significance and $P$-Values,” with six principles underlying the proper use and interpretation of $p$-values. The ASA released this guidance on $p$-values to improve the conduct and interpretation of quantitative science and to inform the growing emphasis on reproducibility of science research.

We as authors much prefer the use of confidence intervals for statistical inference, since in our opinion they are much less prone to large misinterpretation. However, many fields still exclusively use $p$-values for statistical inference and this is one reason for including them in this text. We encourage you to learn more about “p-hacking” as well and its implication for science.

9.7.4 Additional resources

An R script file of all R code used in this chapter is available here.

If you want more examples of the infer workflow for conducting hypothesis tests, we suggest you check out the infer package homepage, in particular, a series of example analyses available at https://infer.netlify.app/articles/.

9.7.5 What’s to come

We conclude with the infer pipeline for hypothesis testing in Figure 9.17.

FIGURE 9.17: infer package workflow for hypothesis testing.

Now that we have armed ourselves with an understanding of confidence intervals from Chapter 8 and hypothesis tests from this chapter, we will now study inference for regression in the upcoming Chapter 10.

8 Estimation, Confidence Intervals, and Bootstrapping

10 Inference for Regression

Scenario	Population parameter	Notation	Point estimate	Symbol(s)
1	Population proportion	\(p\)	Sample proportion	\(\widehat{p}\)
2	Population mean	\(\mu\)	Sample mean	\(\overline{x}\) or \(\widehat{\mu}\)
3	Difference in population proportions	\(p_1 - p_2\)	Difference in sample proportions	\(\widehat{p}_1 - \widehat{p}_2\)

9 Hypothesis Testing

Needed packages

9.1 Tying confidence intervals to hypothesis testing

9.1.1 The one-sample hypothesis test for the population mean

The theory-based approach

The simulation-based approach

9.1.2 Hypothesis tests and confidence intervals

9.2 Music popularity activity

9.2.1 Is metal music more popular than deep house music?

9.2.2 Shuffling once

9.2.3 What did we just do?

9.3 Understanding hypothesis tests

9.4 Conducting hypothesis tests

9.4.1 infer package workflow

1. specify variables

2. hypothesize the null

3. generate replicates

4. calculate summary statistics

5. visualize the p-value

9.4.2 Comparison with confidence intervals

9.4.3 There is only one test

9.5 Interpreting hypothesis tests

9.5.1 Two possible outcomes

9.5.2 Types of errors

9.5.3 How do we choose alpha?

9.6 Case study: are action or romance movies rated higher?

9.6.1 IMDb ratings data

9.6.2 Sampling scenario

9.6.3 Conducting the hypothesis test

1. specify variables

2. hypothesize the null

3. generate replicates

4. calculate summary statistics

5. visualize the p-value

9.7 Summary and Final Remarks

9.7.1 Theory-based approach for two-sample hypothesis tests

Welch’s two-sample t-statistic

9.7.2 When inference is not needed

9.7.3 Problems with p-values

9.7.4 Additional resources

9.7.5 What’s to come

9.4.1 `infer` package workflow

1. `specify` variables

2. `hypothesize` the null

3. `generate` replicates

4. `calculate` summary statistics

5. `visualize` the p-value

1. `specify` variables

2. `hypothesize` the null

3. `generate` replicates

4. `calculate` summary statistics

5. `visualize` the p-value