
A Statistical Background
A.1 Basic statistical terms
Note that all the following statistical terms apply only to numerical variables, except the distribution which can exist for both numerical and categorical variables.
A.1.1 Mean
The mean is the most commonly reported measure of center. It is commonly called the average though this term can be a little ambiguous. The mean is the sum of all of the data elements divided by how many elements there are. If we have \(n\) data points, the mean is given by:
\[Mean = \frac{x_1 + x_2 + \cdots + x_n}{n}\]
A.1.2 Median
The median is calculated by first sorting a variable’s data from smallest to largest. After sorting the data, the middle element in the list is the median. If the middle falls between two values, then the median is the mean of those two middle values.
A.1.3 Standard deviation and variance
We will next discuss the standard deviation (\(sd\)) of a variable. The formula can be a little intimidating at first but it is important to remember that it is essentially a measure of how far we expect a given data value will be from its mean:
\[sd = \sqrt{\frac{(x_1 - Mean)^2 + (x_2 - Mean)^2 + \cdots + (x_n - Mean)^2}{n - 1}}\]
The variance of a variable is merely the standard deviation squared.
\[variance = sd^2 = \frac{(x_1 - Mean)^2 + (x_2 - Mean)^2 + \cdots + (x_n - Mean)^2}{n - 1}\]
A.1.4 Five-number summary
The five-number summary consists of five summary statistics: the minimum, the first quantile AKA 25th percentile, the second quantile AKA median or 50th percentile, the third quantile AKA 75th, and the maximum. The five-number summary of a variable is used when constructing boxplots, as seen in Section 2.7.
The quantiles are calculated as
- first quantile (\(Q_1\)): the median of the first half of the sorted data
- third quantile (\(Q_3\)): the median of the second half of the sorted data
The interquartile range (IQR) is defined as \(Q_3 - Q_1\) and is a measure of how spread out the middle 50% of values are. The IQR corresponds to the length of the box in a boxplot.
The median and the IQR are not influenced by the presence of outliers in the ways that the mean and standard deviation are. They are, thus, recommended for skewed datasets. We say in this case that the median and IQR are more robust to outliers.
A.1.5 Distribution
The distribution of a variable shows how frequently different values of a variable occur. Looking at the visualization of a distribution can show where the values are centered, show how the values vary, and give some information about where a typical value might fall. It can also alert you to the presence of outliers.
Recall from Chapter 2 that we can visualize the distribution of a numerical variable using binning in a histogram and that we can visualize the distribution of a categorical variable using a barplot.
A.2 Normal distribution
Let’s next discuss one particular kind of distribution: normal distributions. Such bell-shaped distributions are defined by two values: (1) the mean \(\mu\) (“mu”) which locates the center of the distribution and (2) the standard deviation \(\sigma\) (“sigma”) which determines the variation of the distribution. In Figure A.1, we plot three normal distributions where:
- The solid normal curve has mean \(\mu = 5\) & standard deviation \(\sigma = 2\).
- The dotted normal curve has mean \(\mu = 5\) & standard deviation \(\sigma = 5\).
- The dashed normal curve has mean \(\mu = 15\) & standard deviation \(\sigma = 2\).
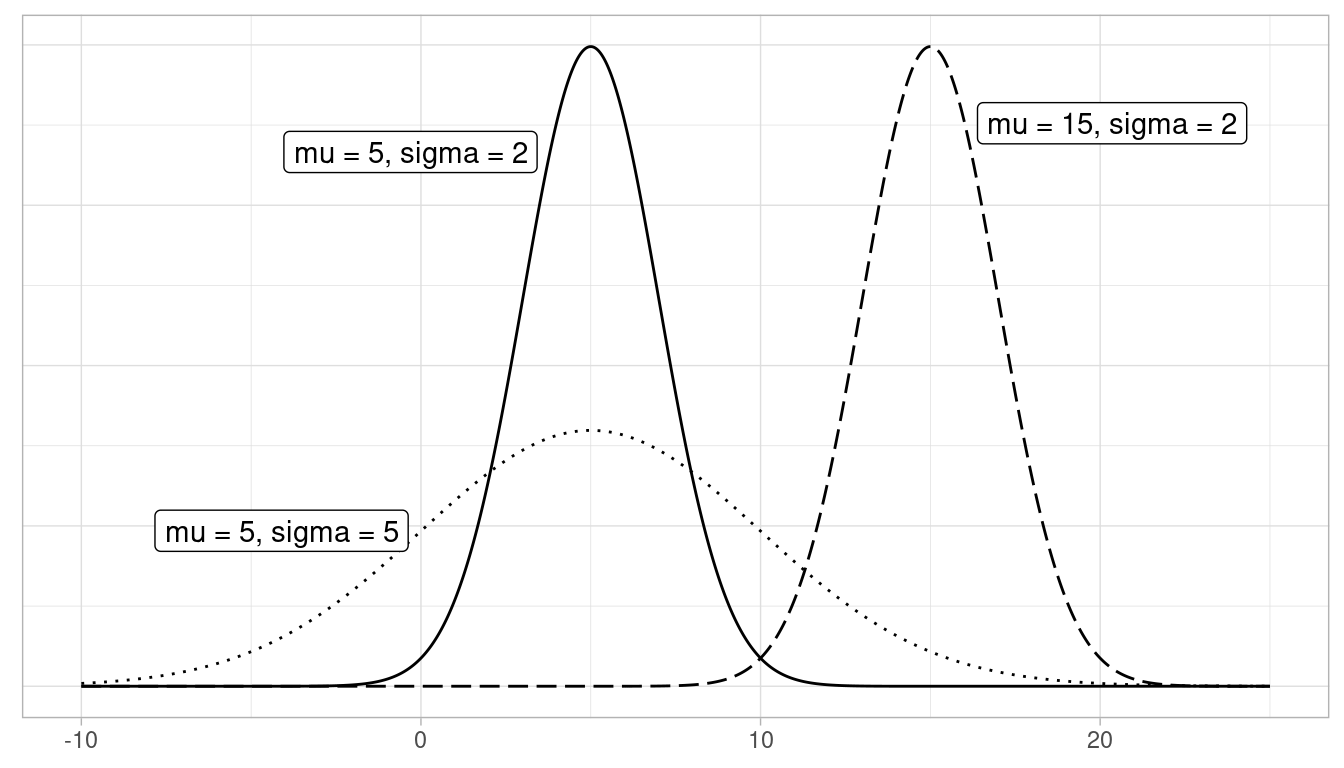
FIGURE A.1: Three normal distributions.
Notice how the solid and dotted line normal curves have the same center due to their common mean \(\mu\) = 5. However, the dotted line normal curve is wider due to its larger standard deviation of \(\sigma\) = 5. On the other hand, the solid and dashed line normal curves have the same variation due to their common standard deviation \(\sigma\) = 2. However, they are centered at different locations.
When the mean \(\mu\) = 0 and the standard deviation \(\sigma\) = 1, the normal distribution has a special name. It’s called the standard normal distribution or the \(z\)-curve.
Furthermore, if a variable follows a normal curve, there are three rules of thumb we can use:
- 68% of values will lie within \(\pm\) 1 standard deviation of the mean.
- 95% of values will lie within \(\pm\) 1.96 \(\approx\) 2 standard deviations of the mean.
- 99.7% of values will lie within \(\pm\) 3 standard deviations of the mean.
Let’s illustrate this on a standard normal curve in Figure A.2. The dashed lines are at -3, -1.96, -1, 0, 1, 1.96, and 3. These 7 lines cut up the x-axis into 8 segments. The areas under the normal curve for each of the 8 segments are marked and add up to 100%. For example:
- The middle two segments represent the interval -1 to 1. The shaded area above this interval represents 34% + 34% = 68% of the area under the curve. In other words, 68% of values.
- The middle four segments represent the interval -1.96 to 1.96. The shaded area above this interval represents 13.5% + 34% + 34% + 13.5% = 95% of the area under the curve. In other words, 95% of values.
- The middle six segments represent the interval -3 to 3. The shaded area above this interval represents 2.35% + 13.5% + 34% + 34% + 13.5% + 2.35% = 99.7% of the area under the curve. In other words, 99.7% of values.
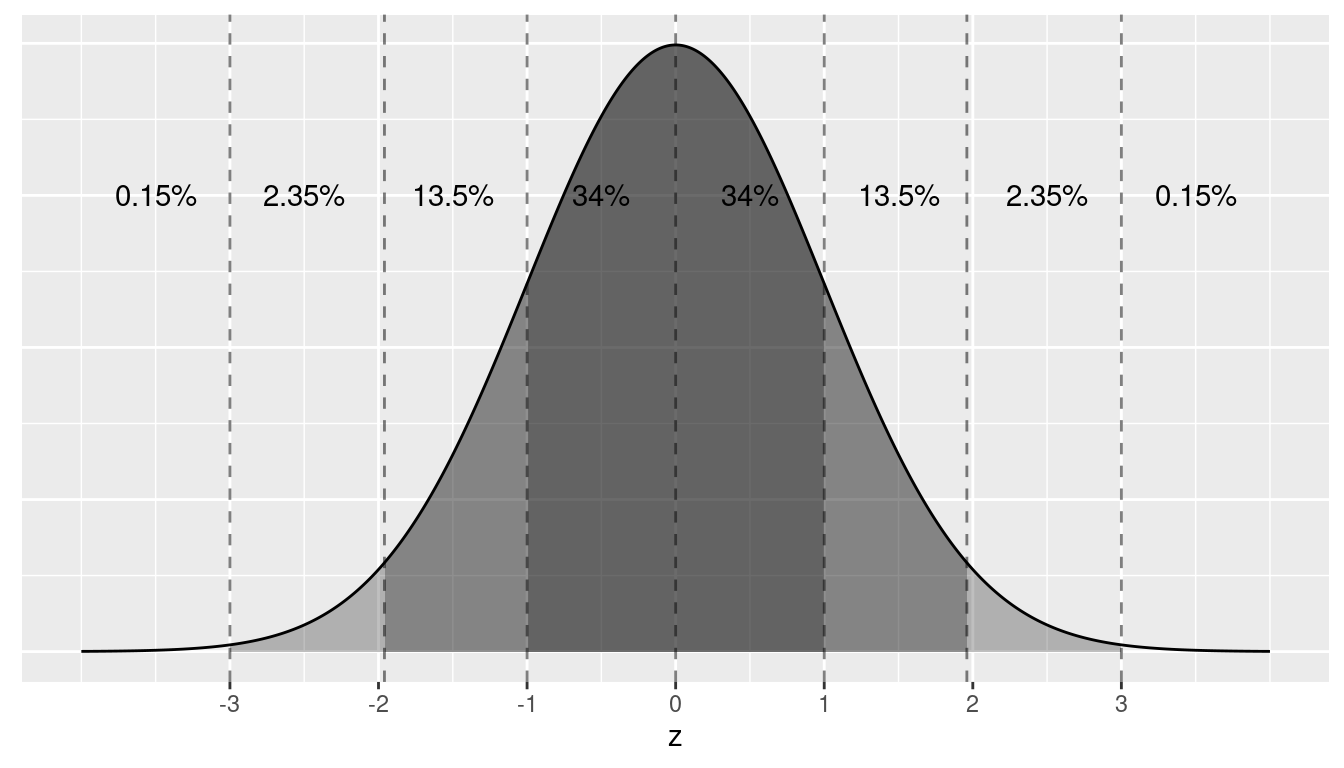
FIGURE A.2: Rules of thumb about areas under normal curves.
Learning check
Say you have a normal distribution with mean \(\mu = 6\) and standard deviation \(\sigma = 3\).
(LCA.1) What proportion of the area under the normal curve is less than 3? Greater than 12? Between 0 and 12?
(LCA.2) What is the 2.5th percentile of the area under the normal curve? The 97.5th percentile? The 100th percentile?
A.3 log10 transformations
At its simplest, log10 transformations return base 10 logarithms. For example, since \(1000 = 10^3\), running log10(1000) returns 3 in R. To undo a log10 transformation, we raise 10 to this value. For example, to undo the previous log10 transformation and return the original value of 1000, we raise 10 to the power of 3 by running 10^(3) = 1000 in R.
Log transformations allow us to focus on changes in orders of magnitude. In other words, they allow us to focus on multiplicative changes instead of additive ones. Let’s illustrate this idea in Table A.1 with examples of prices of consumer goods in 2019 US dollars.
| Price | log10(Price) | Order of magnitude | Examples |
|---|---|---|---|
| $1 | 0 | Singles | Cups of coffee |
| $10 | 1 | Tens | Books |
| $100 | 2 | Hundreds | Mobile phones |
| $1,000 | 3 | Thousands | High definition TVs |
| $10,000 | 4 | Tens of thousands | Cars |
| $100,000 | 5 | Hundreds of thousands | Luxury cars and houses |
| $1,000,000 | 6 | Millions | Luxury houses |
Let’s make some remarks about log10 transformations based on Table A.1:
- When purchasing a cup of coffee, we tend to think of prices ranging in single dollars, such as $2 or $3. However, when purchasing a mobile phone, we don’t tend to think of their prices in units of single dollars such as $313 or $727. Instead, we tend to think of their prices in units of hundreds of dollars like $300 or $700. Thus, cups of coffee and mobile phones are of different orders of magnitude in price.
- Let’s say we want to know the log10 transformed value of $76. This would be hard to compute exactly without a calculator. However, since $76 is between $10 and $100 and since log10(10) = 1 and log10(100) = 2, we know log10(76) will be between 1 and 2. In fact, log10(76) is 1.880814.
- log10 transformations are monotonic, meaning they preserve orders. So if Price A is lower than Price B, then log10(Price A) will also be lower than log10(Price B).
- Most importantly, increments of one in log10-scale correspond to relative multiplicative changes in the original scale and not absolute additive changes. For example, increasing a log10(Price) from 3 to 4 corresponds to a multiplicative increase by a factor of 10: $100 to $1000.
